- Circular Single Linked List, Doubly Linked List, & Circular Doubly Linked List
- Stack & Queue
- Hashing Table & Binary Tree
- Binary Search Tree
Circular Single Linked List
• In circular, last node contains a pointer to the first node
• We can have a circular singly linked list as well as a circular doubly linked list.
• There is no storing of NULL values in the list

Advantages of Circular Linked Lists:
1) Any node can be a starting point.
2) Useful for implementation of queue.
3) Circular lists are useful in applications to repeatedly go around the list.
4) Circular Doubly Linked Lists are used for implementation of advanced data structures like Fibonacci Heap.
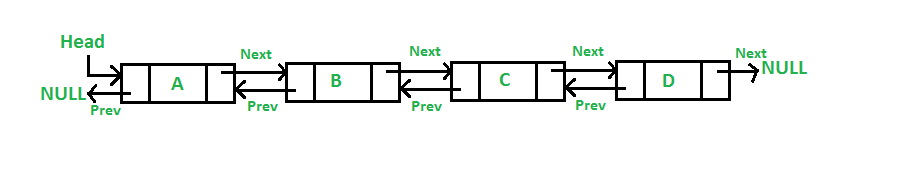
Doubly Linked List
Double/Doubly linked list (DLL) or two-way linked list is a linked list data structure with
two link, one that contain reference to the next data and one that contain reference to the
previous data.
};
Advantages over singly linked list:
1) A DLL can be traversed in both forward and backward direction.
2) The delete operation in DLL is more efficient if pointer to the node to be deleted is given.
3) We can quickly insert a new node before a given node.
Disadvantages over singly linked list:
1) Every node of DLL Require extra space for an previous pointer.
2) All operations require an extra pointer previous to be maintained.
Doubly Linked List: Insertion
A node can be added in four ways:
1) At the front of the DLL.
2) After a given node.
3) At the end of the DLL.
4) Before a given node.
Doubly Linked List: Deletion
There are 4 conditions we should pay attention when deleting:
1) The node to be deleted is the only node in linked list.
2) The node to be deleted is head.
3) The node to be deleted is tail.
4) The node to be deleted is not head or tail.
Circular Doubly Linked List
Circular Doubly Linked List has properties of both doubly linked list and circular linked list in
which two consecutive elements are linked or connected by previous and next pointer and
the last node points to first node by next pointer and also the first node points to last node
by previous pointer.
Stacks Concept
A stack is a container of objects that are inserted and removed according to the last-in first-out (LIFO) principle. In the pushdown stacks only two operations are allowed: push the item into the stack, and pop the item out of the stack. A stack is a limited access data structure - elements can be added and removed from the stack only at the top. push adds an item to the top of the stack, pop removes the item from the top. A helpful analogy is to think of a stack of books; you can remove only the top book, also you can add a new book on the top.A stack is a recursive data structure. Here is a structural definition of a Stack:
a stack is either empty or it consistes of a top and the rest which is a stack;
 Prefix, Infix, & Postfix
1. Prefix adalah notasi yang terbentuk atas
operator dengan operand, dimana oprator
didepan operand.
Contoh: A + B * C (infix).
maka notasi prefixnya adalah: +A*BC.
Pemecahannya:
Diketahui ada 3 operand yaitu: A, B, C dan 2
operand yaitu: +, *.proses dimulai dengan
melihat dari hirarkhi oprator.Contoh diatas operator yang tertinggi adalah * kemudian +. Tanda * diapit oleh 2 operand yaitu B*C, prefixnya dengan menggabungkan operand dan memindahkan operator ke depan dari operand,sehingga fungsi B*C, notasi prefixnya menjadi *BC, sehingga hasil sementara dari notasi prefix adalah A+*BC.
Selanjutnya mencari prefix untuk operator yang berikutnya yaitu +, cara yang dilakukan sama seperti diatas, operator + diapit oleh operand, yaitu A dan *BC, gabungkan operand,sehingga menjadi A*BC,lalu pindahkan operator kedepan operand,sehingga hasil akhir menjadi +A*BC.
2.Infix adalah notasi yang membentuk atas operator dengan operand,dimana operator berada diantara operand.
Contoh : - A + B * C
- (A + B) * C
- A - (B + C) * D ^ E
3.Postfix adalah notasi yang membentuk atas operator dengan operand, dimana operator berada dibelakang operand.
Contoh : A + B * C (infix).
maka notasi postfix adalah ABC*+.
Pemecahannya:
Diketahui ada 3 operand yaitu : A,B,C dan 2 operator yaitu : +, *. proses dimulai dengan melihat dari hirarkhi operator.Contoh diatas operator yang tertinggi adalah * kemudian +.
Tanda * diapit oleh kedua operand yaitu B dan C yaitu B*C, postfix dengan menggabungkan operand B dan C menjadi BC,lalu memindahkan operator ke belakang operand C, sehingga fungsi B*C, notasi postfixnya menjadi BC*.Sehingga hasil sementara dari notasi postfix adalah A + BC*.
Selanjutnya mencari postfix untuk operator yang berikutnya, yaitu +, dengan cara yang dilakukan sama seperti di atas, operator + diapit oleh 2 operand, yaitu A dan BC*. Gabungkan operand tersebut, sehingga menjadi ABC*, lalu pindahkan operator + kebelakang operand ABC*.
Sehingga hasil akhir menjadi ABC*+.
Stack Applications
Stacks are widely used to:
• Reverse the order of data
• Convert infix expression into postfix
• Convert postfix expression into infix
• Backtracking problem
• System stack is used in every recursive function
• Converting a decimal number into its binary equivalent
Queue Concept
A Queue is a linear structure which follows
particular order in which the operations are performed. The order is First In First Out (FIFO). A good example of a queue is any queue of consumers for a resource where the consumer that came first is served first. The difference between stacks and queues is in removing. In a stack we remove the item the most recently added; in a queue, we remove the item the least recently added. 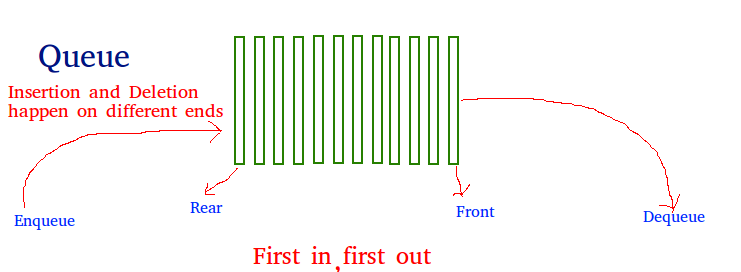
Circular Queue
Circular Queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle and the last position is connected back to the first position to make a circle. It is also called ‘Ring Buffer’.

In a normal Queue, we can insert elements until queue becomes full. But once queue becomes full, we can not insert the next element even if there is a space in front of queue.
Priority Queue
Priority Queue is an extension of queue with following properties.
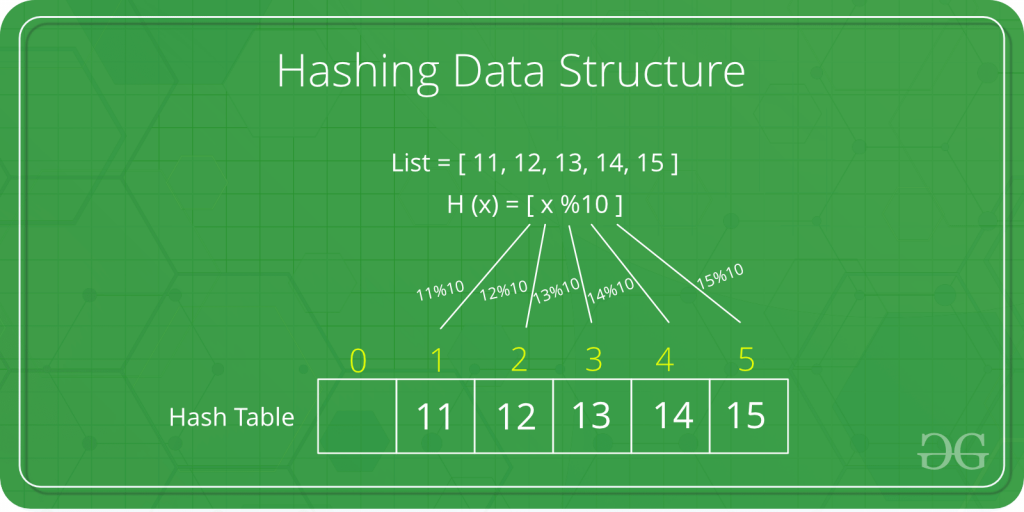
Hashing
Hashing adalah teknik yang digunakan untuk menyimpan dan mengambil kunci dengan cepat. Dalam hashing, string karakter ditransformasikan menjadi nilai panjang yang biasanya lebih pendek atau kunci yang mewakili string asli. Hashing digunakan untuk mengindeks dan mengambil item dalam database karena lebih cepat menemukan item menggunakan kunci hash yang lebih pendek daripada menemukannya menggunakan nilai asli. Hashing juga dapat didefinisikan sebagai konsep mendistribusikan kunci dalam array yang disebut tabel hash menggunakan fungsi yang telah ditentukan yang disebut fungsi hash.
Hash Table
Hash table adalah struktur data yang mengimplementasikan tipe data abstrak array asosiatif, struktur yang dapat memetakan kunci ke nilai. Tabel hash menggunakan fungsi hash untuk menghitung indeks, juga disebut kode hash, ke dalam array dari ember atau slot, dari mana nilai yang diinginkan dapat ditemukan.
Implementasi Hash Table pada Blockchain
Peran penting kriptografi dalam jaringan blockchain terus berkembang tiada hentinya. Salah satunya adalah proses perhitungan sebuah data secara konkret dan unik. Metode ini dikenal dengan Hash, mungkin anda tak asing dengan kode unik yang banyak ditemukan di Blockchain dan itulah salah satu contoh Hash.
Nilai berharga sebuah data saat ini berpotensi dibobol atau diketahui oleh orang lain. Salah satu teknik mengakalinya ialah dengan pemberian kode unik. Ibarat peran dari sidik jari elektronik (digital fingerprint) pada data digital punya Anda.
Data tersebut akan aman dan pastinya menjadi orisinalitas data dari orang lain. Hanya orang yang terkait berhak dan bisa masuk ke akses data tersebut. Saat ini beragam proses pengamanan data, mulai dari sidik jari, sidik mata, dan di sistem Blockchain menggunakan kode unik (Hash).
Password atau kode unik di blockchain punya nilai karakter yang lebih panjang dan menggunakan kode unik. Pastinya proses peretesan dengan aplikasi tebak saat ini jelas sangat lama dan bahkan mustahil. Itulah yang menjadi alasan bahwa Hash sangat penting dan dinilai sangat aman.
Tak hanya itu saja, Hash mampu mengubah setiap data yang mengalami perubahan dengan nilai unik sendiri. Ini yang tidak didapatkan pada jaringan biasa. Selain itu, setiap data dokumen dengan panjang berapa pun akan menghasilkan nilai hash yang punya nilai panjang berbeda tergantung spesifikasi Hash yang digunakan.
Monero menilai bahwa perlu adanya keamanan khusus dan beragam pada Hash. Inilah yang menjadi dasar lahirnya konsep CryptoNote. Pengguna yang mengirimkan transaksi atau data tidak dapat diidentifikasi oleh publik karena ada beberapa kunci tersebut. Ia kata sebagai pengalih dan membuat Anda sulit diintai dan data serta privasi tetap aman di jaringan Blockchain.
Implementasi Hash Table di C menggunakan array
Example
#include<stdio.h>
#define size 7
int arr[size];
void init()
{
int i;
for(i = 0; i < size; i++)
arr[i] = -1;
}
void insert(int value)
{
int key = value % size;
if(arr[key] == -1)
{
arr[key] = value;
printf("%d inserted at arr[%d]\n", value,key);
}
else
{
printf("Collision : arr[%d] has element %d already!\n",key,arr[key]);
printf("Unable to insert %d\n",value);
}
}
void del(int value)
{
int key = value % size;
if(arr[key] == value)
arr[key] = -1;
else
printf("%d not present in the hash table\n",value);
}
void search(int value)
{
int key = value % size;
if(arr[key] == value)
printf("Search Found\n");
else
printf("Search Not Found\n");
}
void print()
{
int i;
for(i = 0; i < size; i++)
printf("arr[%d] = %d\n",i,arr[i]);
}
int main()
{
init();
insert(10); //key = 10 % 7 ==> 3
insert(4); //key = 4 % 7 ==> 4
insert(2); //key = 2 % 7 ==> 2
insert(3); //key = 3 % 7 ==> 3 (collision)
printf("Hash table\n");
print();
printf("\n");
printf("Deleting value 10..\n");
del(10);
printf("After the deletion hash table\n");
print();
printf("\n");
printf("Deleting value 5..\n");
del(5);
printf("After the deletion hash table\n");
print();
printf("\n");
printf("Searching value 4..\n");
search(4);
printf("Searching value 10..\n");
search(10);
return 0;
}
|
Tree
tree adalah abstract data type (ADT) yang banyak digunakan untuk mensimulasikan struktur hierarki pohon, dengan nilai root dan subtrees of children dengan node parent, direpresentasikan sebagai satu set node yang terhubung.
Struktur data pohon dapat didefinisikan secara rekursif sebagai kumpulan node (dimulai dari simpul akar), di mana setiap simpul adalah struktur data yang terdiri dari suatu nilai, bersama dengan daftar referensi ke node ("children"), dengan kendala yang tidak ada referensi digandakan, dan tidak ada yang menunjuk ke root
Binary Tree
Pohon yang unsurnya paling banyak memiliki 2 children disebut pohon biner (Binery Tree). Karena setiap elemen dalam pohon biner hanya dapat memiliki 2 children, biasanya disebut left children dan right children.
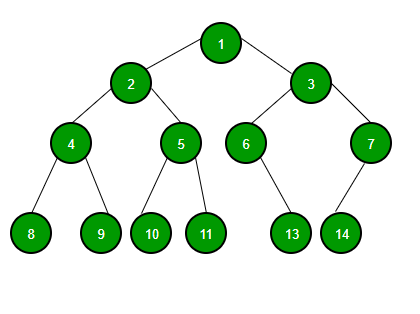
Node Pohon Biner berisi bagian-bagian berikut.
1. Data.
2. Pointer ke left children.
3. Pointer ke right children.
Jenis-jenis Binary Tree :
a) Full Binary Tree
 Binary Tree yang tiap nodenya (kecuali leaf) memiliki dua child dan tiap subtree harus mempunyai panjang path yang sama.
Binary Tree yang tiap nodenya (kecuali leaf) memiliki dua child dan tiap subtree harus mempunyai panjang path yang sama.
b) Complete Binary Tree
Mirip dengan Full Binary Tree, namun tiap subtree boleh memiliki panjang path yang berbeda. Node kecuali leaf memiliki 0 atau 2 child.
c) Skewed Binary Tree
expression tree concept:
Prefix : *+ab/-cde
Postfix : ab+cd-e/*
Infix : (a+b)*((c-d)/e)
https://drive.google.com/open?id=18SQo5RFyK-2cFsNQ42RiRp_zF5hqmhGT
Sekian Summary 1 saya untuk semester 2, mohon maaf bila ada kekurangan, terima kasih.
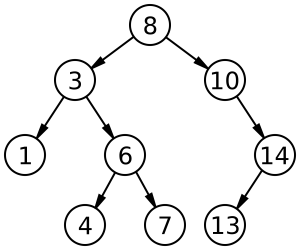
Binary Search Tree
Binary Search Tree adalah struktur data yang mengadopsi konsep Binary Tree namun terdapat aturan bahwa setiap child node sebelah kiri selalu lebih kecil nilainya dari pada root node. Begitu pula sebaliknya, setiap child node sebelah kanan selalu lebih besar nilainya daripada root node.

Binary Search Tree membedakan kiri dan kanan sesuai besaran nilainya untuk memberikan efisiensi terhadap proses searching. Kalau struktur data tree sudah tersusun rapi sesuai aturan binary search tree, proses search akan lebih cepat.
Aturan Binary Search Tree:
- Setiap child node sebelah kiri harus lebih kecil nilainya daripada root nodenya.
- Setiap child node sebelah kanan harus lebih besar nilainya daripada root nodenya.
Kemudian, ada 3 jenis cara untuk melakukan penelusuran data (traversal) pada binary search tree, yaitu:
- Pre Order : Print data, telusur ke kiri, telusur ke kanan.
- In Order : Telusur ke kiri, print data, telusur ke kanan.
- Post Order : Telusur ke kiri, telusur ke kanan, print data.
Binary Search Tree memiliki operasi dasar berikut:
- find (X): cari kunci X di Binary Search Tree.
a. Karena properti Binary Search Tree, finding/searching di Binary Search Tree mudah.
b. Biarkan kunci yang ingin kita cari adalah X.
a. Karena properti Binary Search Tree, finding/searching di Binary Search Tree mudah.
b. Biarkan kunci yang ingin kita cari adalah X.
1. Kita mulai dari root.
2. Jika root berisi X maka pencarian berhasil dihentikan.
3. Jika X kurang dari kunci root, maka cari secara rekursif pada sub tree kiri, jika tidak cari
secara rekursif pada sub tree kanan.
- insert (X): masukkan kunci baru X ke dalam Binary Search Tree.
a. Memasukkan ke dalam Binary Search Tree dilakukan secara rekursif.
b. Biarkan kunci node baru menjadi X,
1. Mulailah dari root.
2. Jika X kurang dari kunci simpul maka masukkan X ke sub tree kiri, jika tidak masukkan X
ke sub tree kanan.
3. Ulangi sampai menemukan simpul kosong untuk meletakkan X (X akan selalu menjadi
leaf baru).
- remove (X): hapus kunci X dari Binary Search Tree.b. Biarkan kunci node baru menjadi X,
1. Mulailah dari root.
2. Jika X kurang dari kunci simpul maka masukkan X ke sub tree kiri, jika tidak masukkan X
ke sub tree kanan.
3. Ulangi sampai menemukan simpul kosong untuk meletakkan X (X akan selalu menjadi
leaf baru).
Ada 3 kasus yang harus dipertimbangkan:
1. Jika kunci ada di leaf, hapus saja node itu.
2. Jika kunci ada di node yang memiliki satu children, hapus node itu dan sambungkan
children-nya ke parent-nya.
children-nya ke parent-nya.
3. Jika kunci ada di node yang memiliki dua children, temukan children paling kanan dari sub
tree kirinya (node P), ganti kuncinya dengan kunci P dan hapus P secara rekursif. (atau
secara alternatif dapat memilih anak paling kiri dari sub tree kanannya).
tree kirinya (node P), ganti kuncinya dengan kunci P dan hapus P secara rekursif. (atau
secara alternatif dapat memilih anak paling kiri dari sub tree kanannya).
Contoh Aplikasi Binary Search Tree:
1. Membangun daftar vocabulary yang merupakan bagian dari inverted index (sebuah struktur
data yang digunakan oleh banyak mesin pencari seperti Google.com, Yahoo.com dan
Ask.com).
data yang digunakan oleh banyak mesin pencari seperti Google.com, Yahoo.com dan
Ask.com).
2. Banyak digunakan dalam bahasa pemrograman untuk mengelola dan membangun dynamic
sets.
sets.
Pembentukan Binary Search Tree
Bila diketahui sederetan data 5, 3, 7, 1, 4, 6, 8, 9 maka pemasukan data tersebut dalam struktur data BST, langkah per langkah, adalah sebagai berikut:
Langkah 1:
Langkah 2:
Pemasukan data 3 disebelah kiri simpul 5 karena 3 < 5. 5 3 5 Struktur Data dan Algoritma 4 Taufik Fuadi Abidin, Irvanizam Zamanhuri, Muhammad Subianto.
Langkah 3:
Langkah 4:
Pemasukan data 1. Karena data 1 lebih kecil dari data di root yaitu 5 maka penelusuran dilanjutkan kesebelah kiri root. Kemudian karena disebelah kiri sudah ada daun dengan nilai 3 dan data 1 lebih kecil dari data 3 maka data 1 disisipkan disebelah kiri simpul 3.
Langkah 5:
Pemasukan data 4. 3 5 7 3 5 7 1 3 5 7 1 4 Struktur Data dan Algoritma 5 Taufik Fuadi Abidin, Irvanizam Zamanhuri, Muhammad Subianto.
Langkah 6:
Pemasukan data 6. Karena data 6 lebih besar dari data di root yaitu 5 maka penelusuran dilanjutkan kesebelah kanan root. Kemudian karena disebelah kanan sudah ada simpul dengan nilai 7 dan data 6 lebih kecil dari data 7 maka data 6 disisipkan disebelah kiri simpul 7.
Langkah 7:
Pemasukan data 8. Karena data 8 lebih besar dari data di root yaitu 5 maka penelusuran dilanjutkan kesebelah kanan root. Kemudian karena disebelah kanan sudah ada simpul dengan nilai 7 dan karena data 8 lebih besar dari data 7 maka data 8 disisipkan disebelah kanan simpul 7. 5 7 6 3 1 4 5 7 6 3 1 4 8 Struktur Data dan Algoritma 6 Taufik Fuadi Abidin, Irvanizam Zamanhuri, Muhammad Subianto.
Langkah 8:
Pemasukan data 9. Karena data 9 lebih besar dari data di root yaitu 5 maka penelusuran dilanjutkan kesebelah kanan root. Kemudian karena disebelah kanan bukan merupakan daun yaitu simpul dengan nilai 7 dan karena data 9 lebih besar dari data 7 penelusuran terus dilanjutkan kesebelah kanan. Selanjutnya ditemukan daun dengan nilai 8, karena data 9 lebih besar dari 8 maka data 9 disisipkan disebelah kanan simpul 8. 5 7 6 3 1 4 8 9.
Berikut adalah contoh implementasi Binary Search Tree pada C beserta searching datanya:#include <stdio.h>
#include <stdlib.h>
//inisialisasi struct
struct data{
int number;
//pointer untuk menampung percabangan kiri dan kanan
data *left, *right;
}*root;
//fungsi push untuk menambah data
void push(data **current, int number){
//jika pointer current kosong maka akan membuat blok data baru
if((*current)==NULL){
(*current) = (struct data *)malloc(sizeof (data));
//mengisi data
(*current)->number=number;
(*current)->left = (*current)->right = NULL;
//jika tidak kosong, maka akan dibandingkan apakah angka yang
//ingin dimasukkan lebih kecil dari pada root
//kalau iya, maka belok ke kiri dan lakukan rekursif
//terus menerus hingga kosong
}else if(number < (*current)->number){
push(&(*current)->left, number);
//jika lebih besar, belok ke kanan
}else if(number >= (*current)->number){
push(&(*current)->right, number);
}
}
//preOrder : cetak, kiri, kanan
void preOrder(data **current){
if((*current)!=NULL){
printf("%d -> ", (*current)->number);
preOrder(&(*current)->left);
preOrder(&(*current)->right);
}
}
//inOrder : kiri, cetak, kanan
void inOrder(data **current){
if((*current)!=NULL){
inOrder(&(*current)->left);
printf("%d -> ", (*current)->number);
inOrder(&(*current)->right);
}
}
//postOrder : kiri, kanan, cetak
void postOrder(data **current){
if((*current)!=NULL){
postOrder(&(*current)->left);
postOrder(&(*current)->right);
printf("%d -> ", (*current)->number);
}
}
//searching data
void search(data **current, int number){
//jika pointer current memiliki data
if((*current)!=NULL){
//cek, apakah datanya lebih kecil. Jika iya, belok ke kiri
if(number<(*current)->number){
search(&(*current)->left,number);
//jika lebih besar, maka belok ke kanan
}else if(number>(*current)->number){
search(&(*current)->right,number);
//jika sama dengan, maka angka ketemu
}else{
printf("Found : %d", (*current)->number);
}
//jika tidak ada data lagi (not found)
}else{
printf("Not Found.");
}
}
int main(){
push(&root, 11);
push(&root, 22);
push(&root, 13);
push(&root, 15);
push(&root, 9);
inOrder(&root);
printf("\n");
preOrder(&root);
printf("\n");
postOrder(&root);
printf("\n");
search(&root,91);
getchar();
}
Berikut adalah link tugas koding untuk market berbasis c yang telah saya buat:https://drive.google.com/open?id=18SQo5RFyK-2cFsNQ42RiRp_zF5hqmhGT
Sekian Summary 1 saya untuk semester 2, mohon maaf bila ada kekurangan, terima kasih.