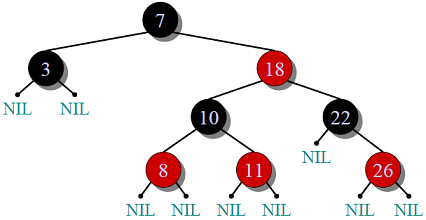
Red-Black Tree
Red-Black Tree is a self-balancing Binary Search Tree where every node follows following rules.
1) Every node has a color either red or black.
2) Root of tree is always black.
3) There are no two adjacent red nodes (A red node cannot have a red parent or red child).
4) Every path from a node (including root) to any of its descendant NULL node has the same number of black nodes.
Why Red-Black Trees?
Most of the BST operations (e.g., search, max, min, insert, delete.. etc) take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed Binary tree. If we make sure that height of the tree remains O(Logn) after every insertion and deletion, then we can guarantee an upper bound of O(Logn) for all these operations. The height of a Red-Black tree is always O(Logn) where n is the number of nodes in the tree.
Most of the BST operations (e.g., search, max, min, insert, delete.. etc) take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed Binary tree. If we make sure that height of the tree remains O(Logn) after every insertion and deletion, then we can guarantee an upper bound of O(Logn) for all these operations. The height of a Red-Black tree is always O(Logn) where n is the number of nodes in the tree.
Comparison with AVL Tree
The AVL trees are more balanced compared to Red-Black Trees, but they may cause more rotations during insertion and deletion. So if your application involves many frequent insertions and deletions, then Red Black trees should be preferred. And if the insertions and deletions are less frequent and search is a more frequent operation, then AVL tree should be preferred over Red-Black Tree.
The AVL trees are more balanced compared to Red-Black Trees, but they may cause more rotations during insertion and deletion. So if your application involves many frequent insertions and deletions, then Red Black trees should be preferred. And if the insertions and deletions are less frequent and search is a more frequent operation, then AVL tree should be preferred over Red-Black Tree.
How does a Red-Black Tree ensure balance?
A simple example to understand balancing is, a chain of 3 nodes is not possible in the Red-Black tree. We can try any combination of colors and see all of them violate Red-Black tree property.
A simple example to understand balancing is, a chain of 3 nodes is not possible in the Red-Black tree. We can try any combination of colors and see all of them violate Red-Black tree property.
A chain of 3 nodes is nodes is not possible in Red-Black Trees.
Following are NOT Red-Black Trees
30 30 30
/ \ / \ / \
20 NIL 20 NIL 20 NIL
/ \ / \ / \
10 NIL 10 NIL 10 NIL
Violates Violates Violates
Property 4. Property 4 Property 3
Following are different possible Red-Black Trees with above 3 keys
20 20
/ \ / \
10 30 10 30
/ \ / \ / \ / \
NIL NIL NIL NIL NIL NIL NIL NIL
From the above examples, we get some idea how Red-Black trees ensure balance. Following is an important fact about balancing in Red-Black Trees.
Black Height of a Red-Black Tree :
Black height is number of black nodes on a path from root to a leaf. Leaf nodes are also counted black nodes. From above properties 3 and 4, we can derive, a Red-Black Tree of height h has black-height >= h/2.
Black height is number of black nodes on a path from root to a leaf. Leaf nodes are also counted black nodes. From above properties 3 and 4, we can derive, a Red-Black Tree of height h has black-height >= h/2.
Number of nodes from a node to its farthest descendant leaf is no more than twice as the number of nodes to the nearest descendant leaf.
Every Red Black Tree with n nodes has height <= 2Log2(n+1)
This can be proved using following facts:
1) For a general Binary Tree, let k be the minimum number of nodes on all root to NULL paths, then n >= 2k – 1 (Ex. If k is 3, then n is at least 7). This expression can also be written as k <= Log2(n+1)
1) For a general Binary Tree, let k be the minimum number of nodes on all root to NULL paths, then n >= 2k – 1 (Ex. If k is 3, then n is at least 7). This expression can also be written as k <= Log2(n+1)
2) From property 4 of Red-Black trees and above claim, we can say in a Red-Black Tree with n nodes, there is a root to leaf path with at-most Log2(n+1) black nodes.
3) From property 3 of Red-Black trees, we can claim that the number black nodes in a Red-Black tree is at least ⌊ n/2 ⌋ where n is the total number of nodes.
From above 2 points, we can conclude the fact that Red Black Tree with n nodes has height <= 2Log2(n+1)
In this post, we introduced Red-Black trees and discussed how balance is ensured. The hard part is to maintain balance when keys are added and removed. We will soon be discussing insertion and deletion operations in coming posts on the Red-Black tree.
Applications :
- Most of the self-balancing BST library functions like map and set in C++ use Red Black Tree
- It is used to implement CPU Scheduling Linux. Completely Fair Scheduler uses it.
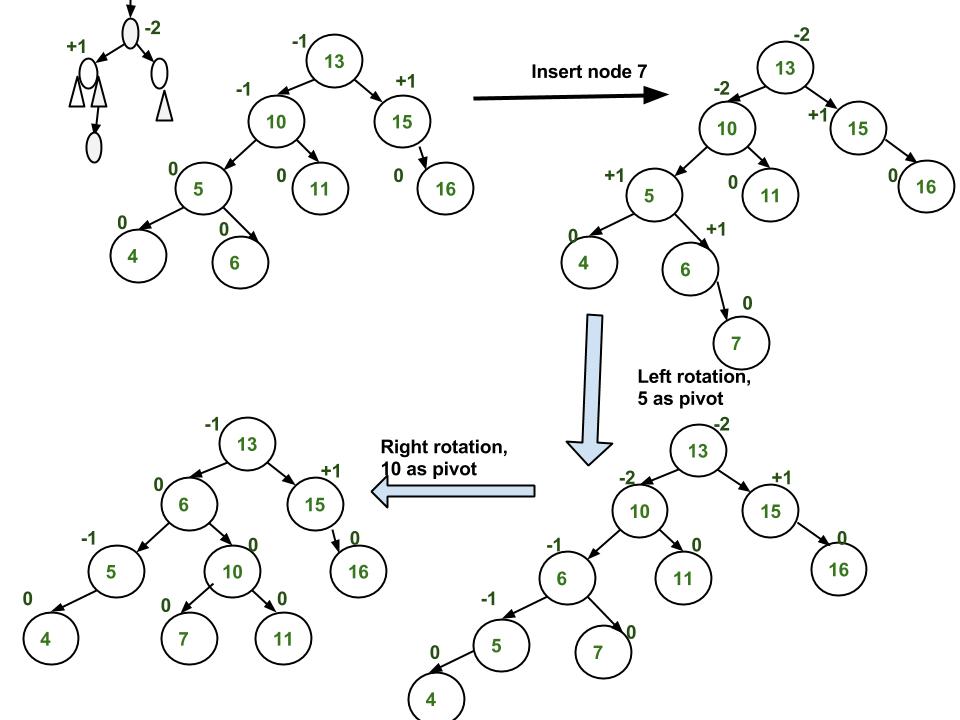
Insertion in RBT
In AVL tree insertion, we used rotation as a tool to do balancing after insertion caused imbalance. In Red-Black tree, we use two tools to do balancing.
1) Recoloring
2) Rotation
2) Rotation
We try recoloring first, if recoloring doesn’t work, then we go for rotation. Following is detailed algorithm. The algorithms has mainly two cases depending upon the color of uncle. If uncle is red, we do recoloring. If uncle is black, we do rotations and/or recoloring. Color of a NULL node is considered as BLACK.
Let x be the newly inserted node.
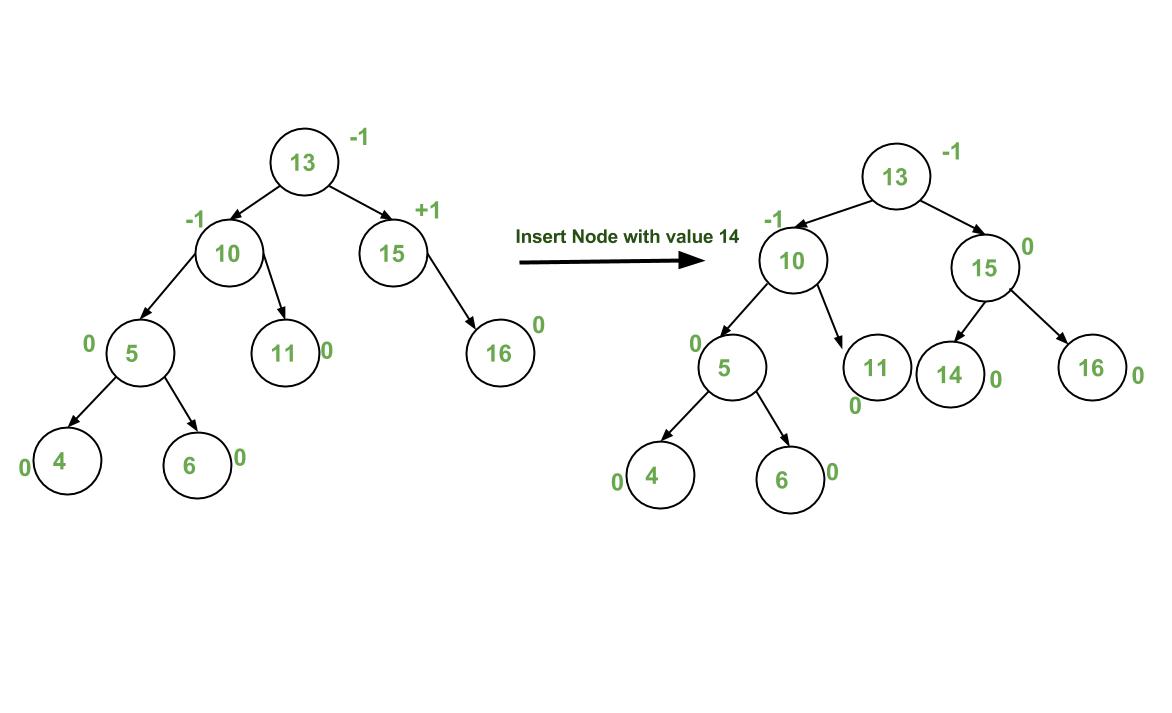
1) Perform standard BST insertion and make the color of newly inserted nodes as RED.
1) Perform standard BST insertion and make the color of newly inserted nodes as RED.
2) If x is root, change color of x as BLACK (Black height of complete tree increases by 1).
3) Do following if color of x’s parent is not BLACK and x is not root.
a) If x’s uncle is RED (Grand parent must have been black from property 4)
(i) Change color of parent and uncle as BLACK.
(ii) color of grand parent as RED.
(iii) Change x = x’s grandparent, repeat steps 2 and 3 for new x.
a) If x’s uncle is RED (Grand parent must have been black from property 4)
(i) Change color of parent and uncle as BLACK.
(ii) color of grand parent as RED.
(iii) Change x = x’s grandparent, repeat steps 2 and 3 for new x.
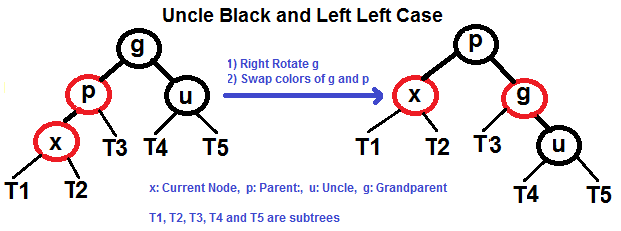
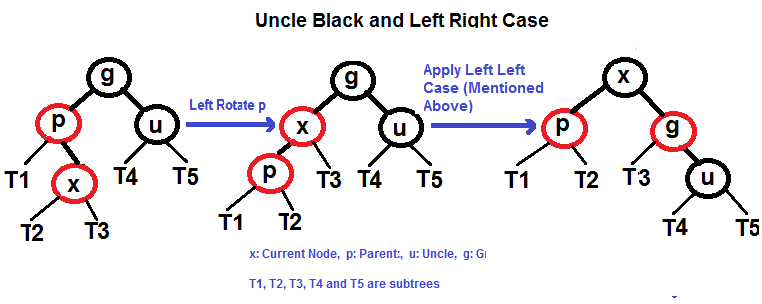
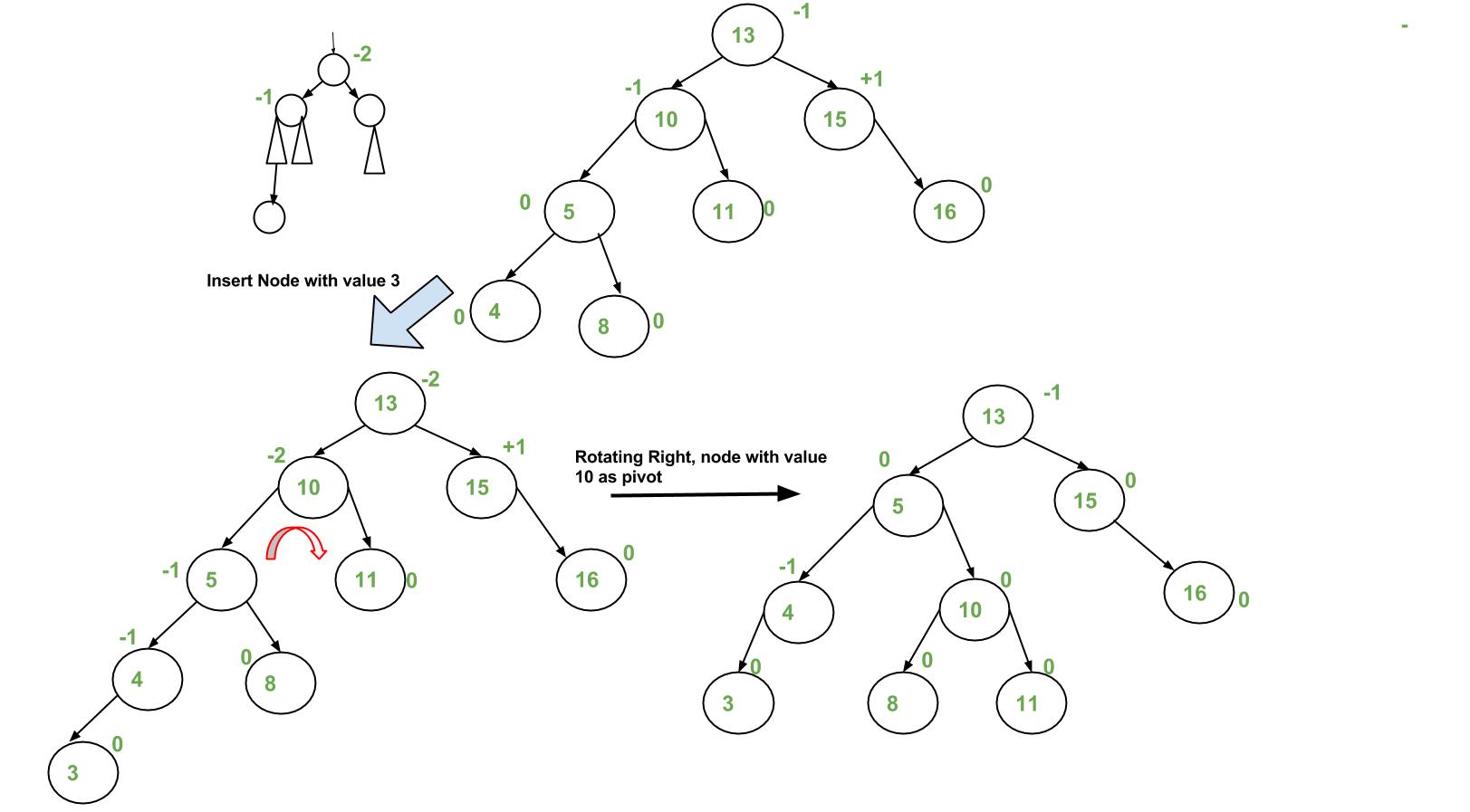
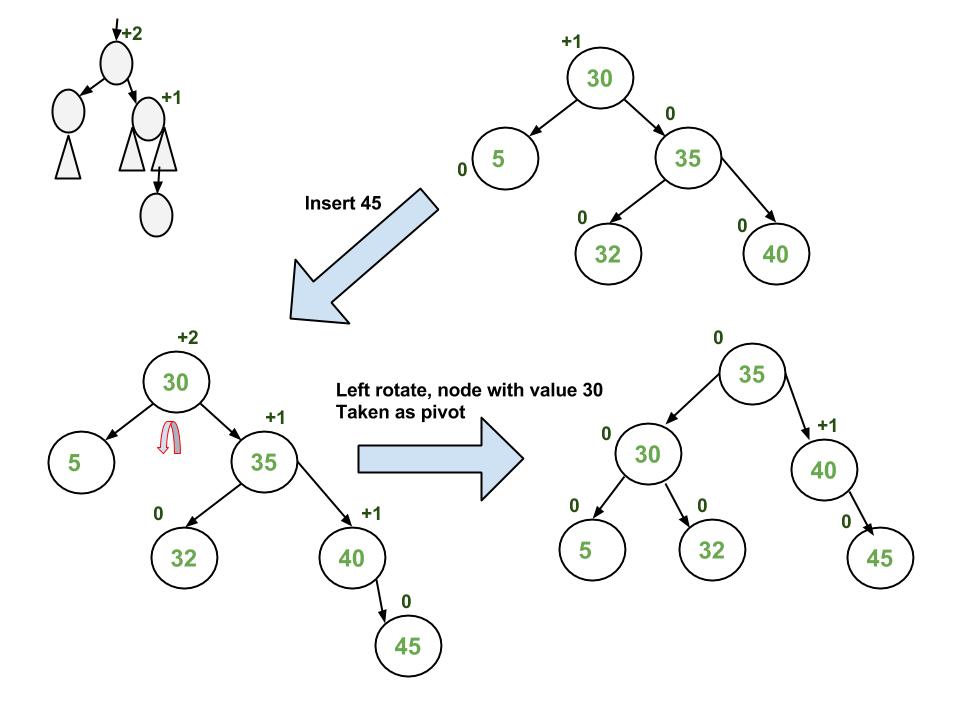
b) If x’s uncle is BLACK, then there can be four configurations for x, x’s parent (p) and x’s grandparent (g) (This is similar to AVL Tree)
i) Left Left Case (p is left child of g and x is left child of p)
ii) Left Right Case (p is left child of g and x is right child of p)
iii) Right Right Case (Mirror of case i)
iv) Right Left Case (Mirror of case ii)
i) Left Left Case (p is left child of g and x is left child of p)
ii) Left Right Case (p is left child of g and x is right child of p)
iii) Right Right Case (Mirror of case i)
iv) Right Left Case (Mirror of case ii)
Following are operations to be performed in four subcases when uncle is BLACK.
All four cases when Uncle is BLACK
Left Left Case (See g, p and x)
Left Left Case (See g, p and x)
Left Right Case (See g, p and x)
Right Right Case (See g, p and x)
Right Left Case (See g, p and x)
Examples of Insertion
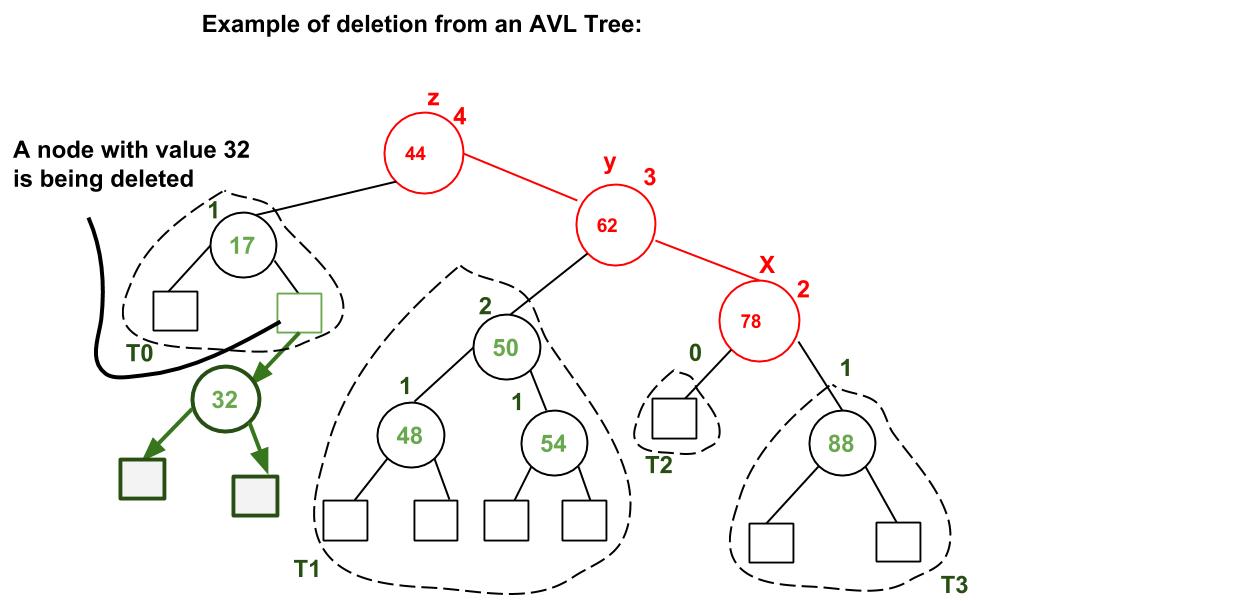
Deletion in RBT
Insertion Vs Deletion:
Like Insertion, recoloring and rotations are used to maintain the Red-Black properties.
Like Insertion, recoloring and rotations are used to maintain the Red-Black properties.
In insert operation, we check color of uncle to decide the appropriate case. In delete operation, we check color of sibling to decide the appropriate case.
The main property that violates after insertion is two consecutive reds. In delete, the main violated property is, change of black height in subtrees as deletion of a black node may cause reduced black height in one root to leaf path.
Deletion is fairly complex process. To understand deletion, notion of double black is used. When a black node is deleted and replaced by a black child, the child is marked as double black. The main task now becomes to convert this double black to single black.
Deletion Steps
Following are detailed steps for deletion.
Following are detailed steps for deletion.
1) Perform standard BST delete. When we perform standard delete operation in BST, we always end up deleting a node which is either leaf or has only one child (For an internal node, we copy the successor and then recursively call delete for successor, successor is always a leaf node or a node with one child). So we only need to handle cases where a node is leaf or has one child. Let v be the node to be deleted and u be the child that replaces v (Note that u is NULL when v is a leaf and color of NULL is considered as Black).
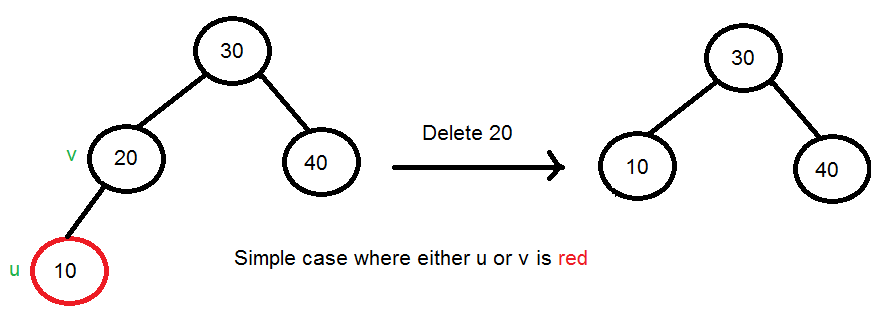
2) Simple Case: If either u or v is red, we mark the replaced child as black (No change in black height). Note that both u and v cannot be red as v is parent of u and two consecutive reds are not allowed in red-black tree.
3) If Both u and v are Black.
3.1) Color u as double black. Now our task reduces to convert this double black to single black. Note that If v is leaf, then u is NULL and color of NULL is considered as black. So the deletion of a black leaf also causes a double black.
3.2) Do following while the current node u is double black and it is not root. Let sibling of node be s.
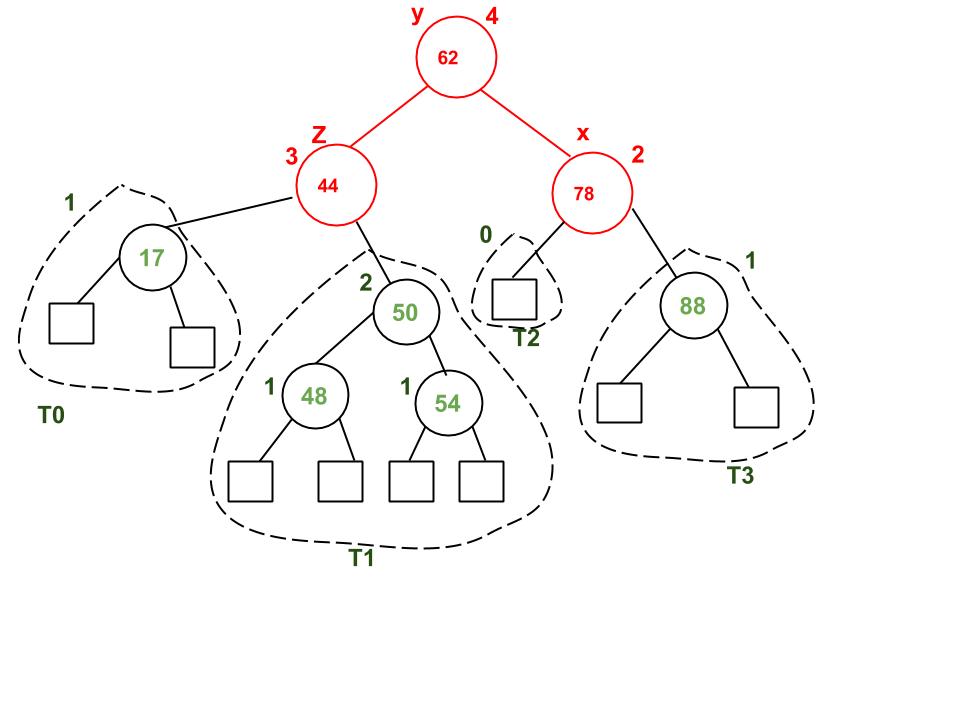
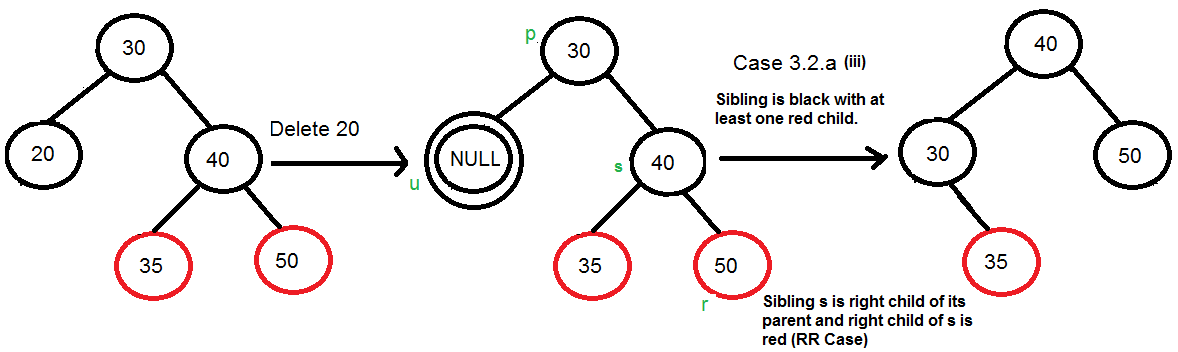
(a) If sibling s is black and at least one of sibling’s children is red, perform rotation(s). Let the red child of s be r. This case can be divided in four subcases depending upon positions of s and r.
(a) If sibling s is black and at least one of sibling’s children is red, perform rotation(s). Let the red child of s be r. This case can be divided in four subcases depending upon positions of s and r.
(i) Left Left Case (s is left child of its parent and r is left child of s or both children of s are red). This is mirror of right right case shown in below diagram.
(ii) Left Right Case (s is left child of its parent and r is right child). This is mirror of right left case shown in below diagram.
(iii) Right Right Case (s is right child of its parent and r is right child of s or both children of s are red)
(iv) Right Left Case (s is right child of its parent and r is left child of s)
(b) If sibling is black and its both children are black, perform recoloring, and recur for the parent if parent is black.
In this case, if parent was red, then we didn’t need to recur for prent, we can simply make it black (red + double black = single black)
In this case, if parent was red, then we didn’t need to recur for prent, we can simply make it black (red + double black = single black)
(c) If sibling is red, perform a rotation to move old sibling up, recolor the old sibling and parent. The new sibling is always black (See the below diagram). This mainly converts the tree to black sibling case (by rotation) and leads to case (a) or (b). This case can be divided in two subcases.
(i) Left Case (s is left child of its parent). This is mirror of right right case shown in below diagram. We right rotate the parent p.
(iii) Right Case (s is right child of its parent). We left rotate the parent p.
(i) Left Case (s is left child of its parent). This is mirror of right right case shown in below diagram. We right rotate the parent p.
(iii) Right Case (s is right child of its parent). We left rotate the parent p.
