AVL Tree
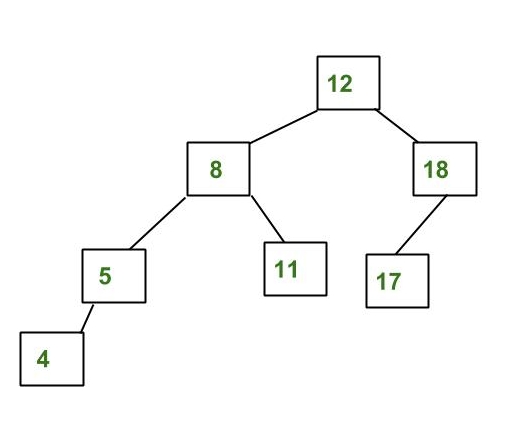
The above tree is AVL because differences between heights of left and right subtrees for every node is less than or equal to 1.
An Example Tree that is NOT an AVL Tree
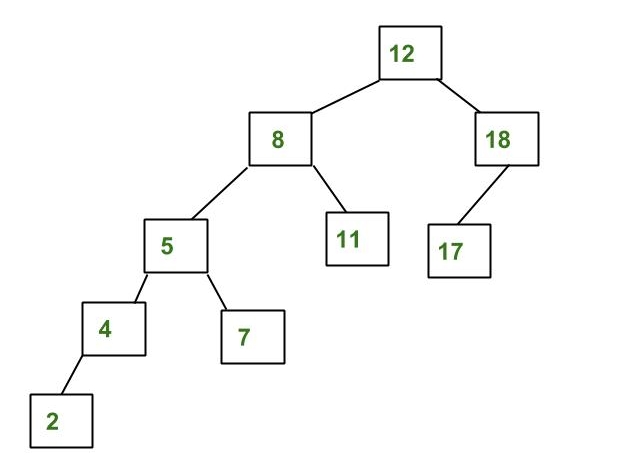
The above tree is not AVL because differences between heights of left and right subtrees for 8 and 18 is greater than 1.
Why AVL Trees?
Most of the BST operations (e.g., search, max, min, insert, delete.. etc) take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed Binary tree. If we make sure that height of the tree remains O(Logn) after every insertion and deletion, then we can guarantee an upper bound of O(Logn) for all these operations. The height of an AVL tree is always O(Logn) where n is the number of nodes in the tree (See this video lecture for proof).
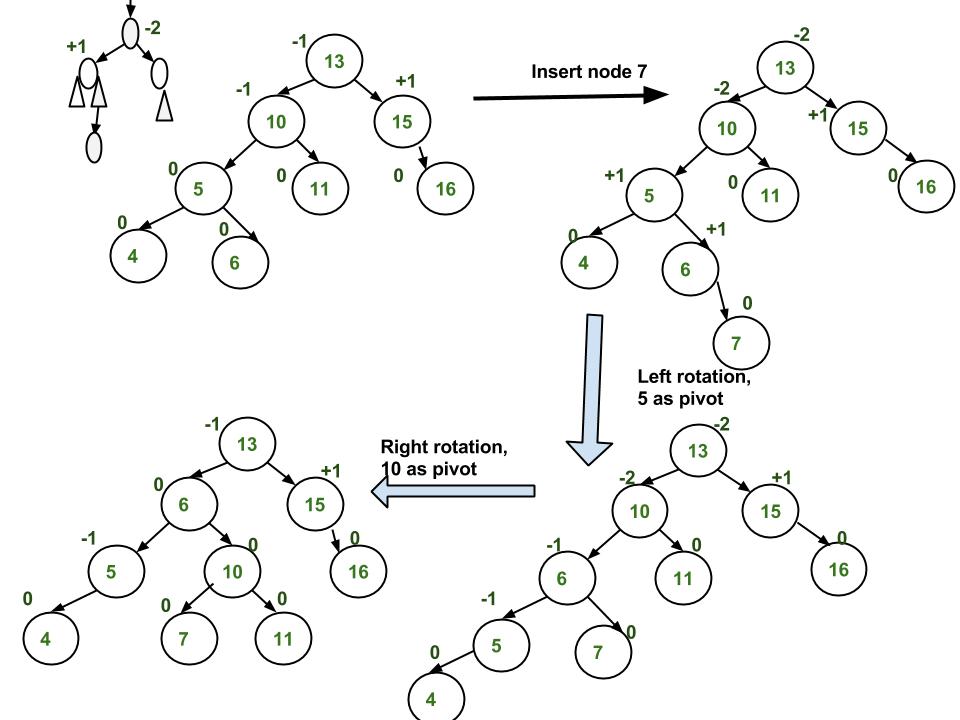
Insertion
To make sure that the given tree remains AVL after every insertion, we must augment the standard BST insert operation to perform some re-balancing. Following are two basic operations that can be performed to re-balance a BST without violating the BST property (keys(left) < key(root) < keys(right)).
1) Left Rotation
2) Right Rotation
T1, T2 and T3 are subtrees of the tree
rooted with y (on the left side) or x (on
the right side)
y x
/ \ Right Rotation / \
x T3 - - - - - - - > T1 y
/ \ < - - - - - - - / \
T1 T2 Left Rotation T2 T3
Keys in both of the above trees follow the
following order
keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
So BST property is not violated anywhere.
Steps to follow for insertion
Let the newly inserted node be w
1) Perform standard BST insert for w.
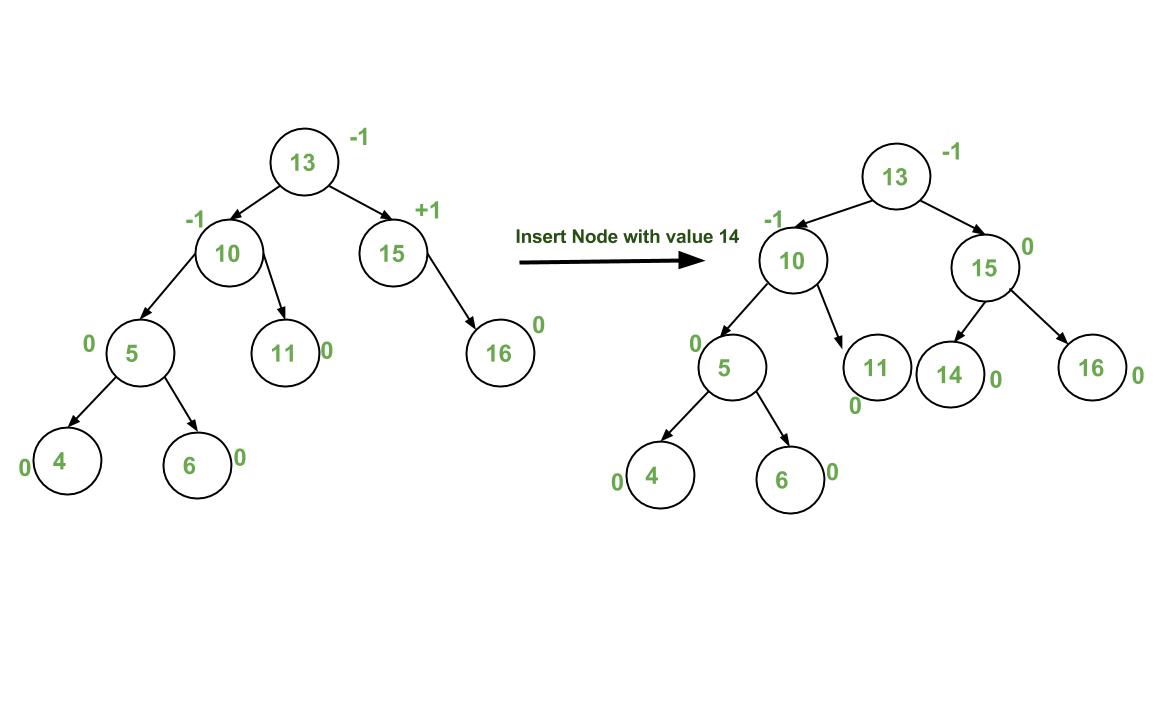
2) Starting from w, travel up and find the first unbalanced node. Let z be the first unbalanced node, y be the child of z that comes on the path from w to z and x be the grandchild of z that comes on the path from w to z.
3) Re-balance the tree by performing appropriate rotations on the subtree rooted with z. There can be 4 possible cases that needs to be handled as x, y and z can be arranged in 4 ways. Following are the possible 4 arrangements:
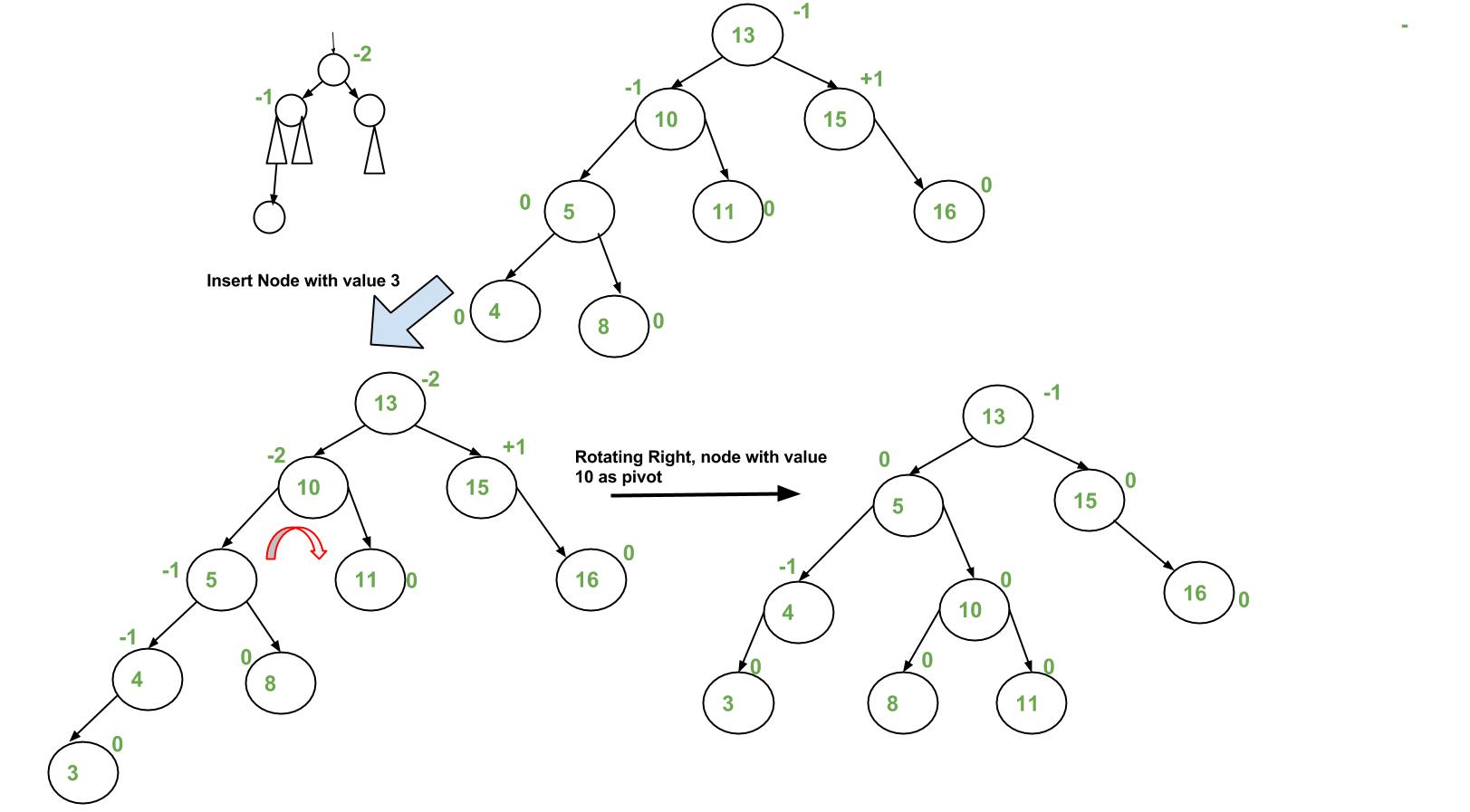
a) y is left child of z and x is left child of y (Left Left Case)
b) y is left child of z and x is right child of y (Left Right Case)
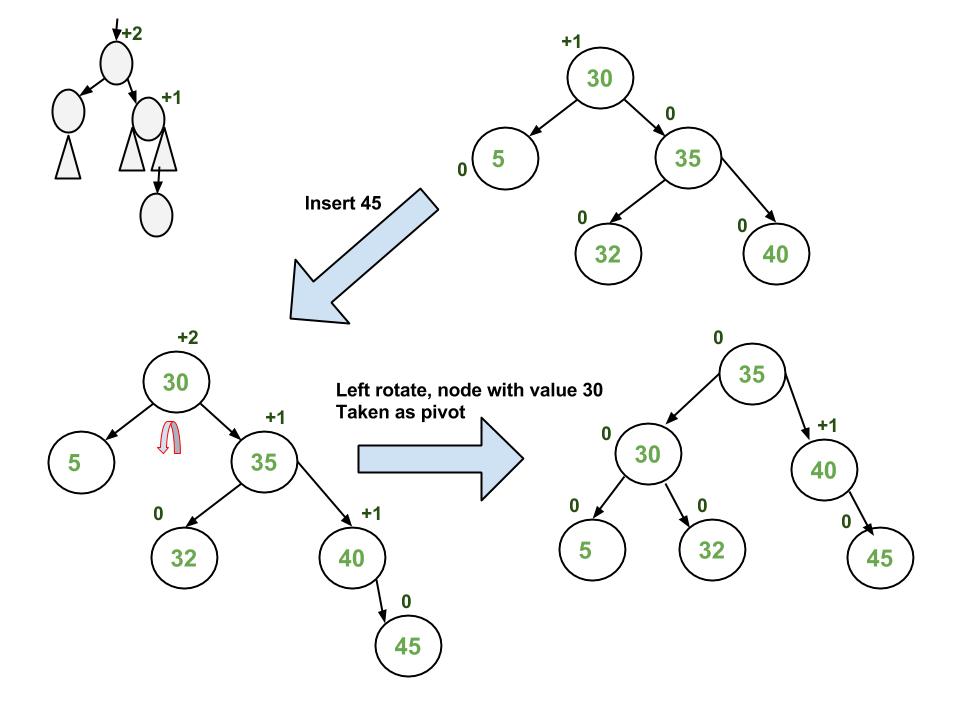
c) y is right child of z and x is right child of y (Right Right Case)
d) y is right child of z and x is left child of y (Right Left Case)
Following are the operations to be performed in above mentioned 4 cases. In all of the cases, we only need to re-balance the subtree rooted with z and the complete tree becomes balanced as the height of subtree (After appropriate rotations) rooted with z becomes same as it was before insertion. (See this video lecture for proof)
a) Left Left Case
T1, T2, T3 and T4 are subtrees.
z y
/ \ / \
y T4 Right Rotate (z) x z
/ \ - - - - - - - - -> / \ / \
x T3 T1 T2 T3 T4
/ \
T1 T2
b) Left Right Case
z z x
/ \ / \ / \
y T4 Left Rotate (y) x T4 Right Rotate(z) y z
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
T1 x y T3 T1 T2 T3 T4
/ \ / \
T2 T3 T1 T2
c) Right Right Case
z y
/ \ / \
T1 y Left Rotate(z) z x
/ \ - - - - - - - -> / \ / \
T2 x T1 T2 T3 T4
/ \
T3 T4
d) Right Left Case
z z x
/ \ / \ / \
T1 y Right Rotate (y) T1 x Left Rotate(z) z y
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
x T4 T2 y T1 T2 T3 T4
/ \ / \
T2 T3 T3 T4
AVL tree is a self-balancing Binary Search Tree (BST) where the difference between heights of left and right subtrees cannot be more than one for all nodes.
An Example Tree that is an AVL Tree

The above tree is AVL because differences between heights of left and right subtrees for every node is less than or equal to 1.

The above tree is AVL because differences between heights of left and right subtrees for every node is less than or equal to 1.
An Example Tree that is NOT an AVL Tree

The above tree is not AVL because differences between heights of left and right subtrees for 8 and 18 is greater than 1.

The above tree is not AVL because differences between heights of left and right subtrees for 8 and 18 is greater than 1.
Why AVL Trees?
Most of the BST operations (e.g., search, max, min, insert, delete.. etc) take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed Binary tree. If we make sure that height of the tree remains O(Logn) after every insertion and deletion, then we can guarantee an upper bound of O(Logn) for all these operations. The height of an AVL tree is always O(Logn) where n is the number of nodes in the tree (See this video lecture for proof).
Most of the BST operations (e.g., search, max, min, insert, delete.. etc) take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed Binary tree. If we make sure that height of the tree remains O(Logn) after every insertion and deletion, then we can guarantee an upper bound of O(Logn) for all these operations. The height of an AVL tree is always O(Logn) where n is the number of nodes in the tree (See this video lecture for proof).
Insertion
To make sure that the given tree remains AVL after every insertion, we must augment the standard BST insert operation to perform some re-balancing. Following are two basic operations that can be performed to re-balance a BST without violating the BST property (keys(left) < key(root) < keys(right)).
1) Left Rotation
2) Right Rotation
To make sure that the given tree remains AVL after every insertion, we must augment the standard BST insert operation to perform some re-balancing. Following are two basic operations that can be performed to re-balance a BST without violating the BST property (keys(left) < key(root) < keys(right)).
1) Left Rotation
2) Right Rotation
T1, T2 and T3 are subtrees of the tree
rooted with y (on the left side) or x (on
the right side)
y x
/ \ Right Rotation / \
x T3 - - - - - - - > T1 y
/ \ < - - - - - - - / \
T1 T2 Left Rotation T2 T3
Keys in both of the above trees follow the
following order
keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
So BST property is not violated anywhere.
Steps to follow for insertion
Let the newly inserted node be w
1) Perform standard BST insert for w.
2) Starting from w, travel up and find the first unbalanced node. Let z be the first unbalanced node, y be the child of z that comes on the path from w to z and x be the grandchild of z that comes on the path from w to z.
3) Re-balance the tree by performing appropriate rotations on the subtree rooted with z. There can be 4 possible cases that needs to be handled as x, y and z can be arranged in 4 ways. Following are the possible 4 arrangements:
a) y is left child of z and x is left child of y (Left Left Case)
b) y is left child of z and x is right child of y (Left Right Case)
c) y is right child of z and x is right child of y (Right Right Case)
d) y is right child of z and x is left child of y (Right Left Case)
Let the newly inserted node be w
1) Perform standard BST insert for w.
2) Starting from w, travel up and find the first unbalanced node. Let z be the first unbalanced node, y be the child of z that comes on the path from w to z and x be the grandchild of z that comes on the path from w to z.
3) Re-balance the tree by performing appropriate rotations on the subtree rooted with z. There can be 4 possible cases that needs to be handled as x, y and z can be arranged in 4 ways. Following are the possible 4 arrangements:
a) y is left child of z and x is left child of y (Left Left Case)
b) y is left child of z and x is right child of y (Left Right Case)
c) y is right child of z and x is right child of y (Right Right Case)
d) y is right child of z and x is left child of y (Right Left Case)
Following are the operations to be performed in above mentioned 4 cases. In all of the cases, we only need to re-balance the subtree rooted with z and the complete tree becomes balanced as the height of subtree (After appropriate rotations) rooted with z becomes same as it was before insertion. (See this video lecture for proof)
a) Left Left Case
T1, T2, T3 and T4 are subtrees.
z y
/ \ / \
y T4 Right Rotate (z) x z
/ \ - - - - - - - - -> / \ / \
x T3 T1 T2 T3 T4
/ \
T1 T2
b) Left Right Case
z z x
/ \ / \ / \
y T4 Left Rotate (y) x T4 Right Rotate(z) y z
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
T1 x y T3 T1 T2 T3 T4
/ \ / \
T2 T3 T1 T2
c) Right Right Case
z y
/ \ / \
T1 y Left Rotate(z) z x
/ \ - - - - - - - -> / \ / \
T2 x T1 T2 T3 T4
/ \
T3 T4
d) Right Left Case
z z x
/ \ / \ / \
T1 y Right Rotate (y) T1 x Left Rotate(z) z y
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
x T4 T2 y T1 T2 T3 T4
/ \ / \
T2 T3 T3 T4
Steps to follow for deletion.
To make sure that the given tree remains AVL after every deletion, we must augment the standard BST delete operation to perform some re-balancing. Following are two basic operations that can be performed to re-balance a BST without violating the BST property (keys(left) < key(root) < keys(right)).
1) Left Rotation
2) Right Rotation
T1, T2 and T3 are subtrees of the tree rooted with y (on left side)
or x (on right side)
y x
/ \ Right Rotation / \
x T3 – - – - – - – > T1 y
/ \ < - - - - - - - / \
T1 T2 Left Rotation T2 T3
Keys in both of the above trees follow the following order
keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
So BST property is not violated anywhere.
Let w be the node to be deleted
1) Perform standard BST delete for w.
2) Starting from w, travel up and find the first unbalanced node. Let z be the first unbalanced node, y be the larger height child of z, and x be the larger height child of y. Note that the definitions of x and y are different from insertion here.
3) Re-balance the tree by performing appropriate rotations on the subtree rooted with z. There can be 4 possible cases that needs to be handled as x, y and z can be arranged in 4 ways. Following are the possible 4 arrangements:
a) y is left child of z and x is left child of y (Left Left Case)
b) y is left child of z and x is right child of y (Left Right Case)
c) y is right child of z and x is right child of y (Right Right Case)
d) y is right child of z and x is left child of y (Right Left Case)
Like insertion, following are the operations to be performed in above mentioned 4 cases. Note that, unlike insertion, fixing the node z won’t fix the complete AVL tree. After fixing z, we may have to fix ancestors of z as well (See this video lecture for proof)
a) Left Left Case
T1, T2, T3 and T4 are subtrees.
z y
/ \ / \
y T4 Right Rotate (z) x z
/ \ - - - - - - - - -> / \ / \
x T3 T1 T2 T3 T4
/ \
T1 T2
b) Left Right Case
z z x
/ \ / \ / \
y T4 Left Rotate (y) x T4 Right Rotate(z) y z
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
T1 x y T3 T1 T2 T3 T4
/ \ / \
T2 T3 T1 T2
c) Right Right Case
z y
/ \ / \
T1 y Left Rotate(z) z x
/ \ - - - - - - - -> / \ / \
T2 x T1 T2 T3 T4
/ \
T3 T4
d) Right Left Case
z z x
/ \ / \ / \
T1 y Right Rotate (y) T1 x Left Rotate(z) z y
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
x T4 T2 y T1 T2 T3 T4
/ \ / \
T2 T3 T3 T4
Unlike insertion, in deletion, after we perform a rotation at z, we may have to perform a rotation at ancestors of z. Thus, we must continue to trace the path until we reach the root.
Example:
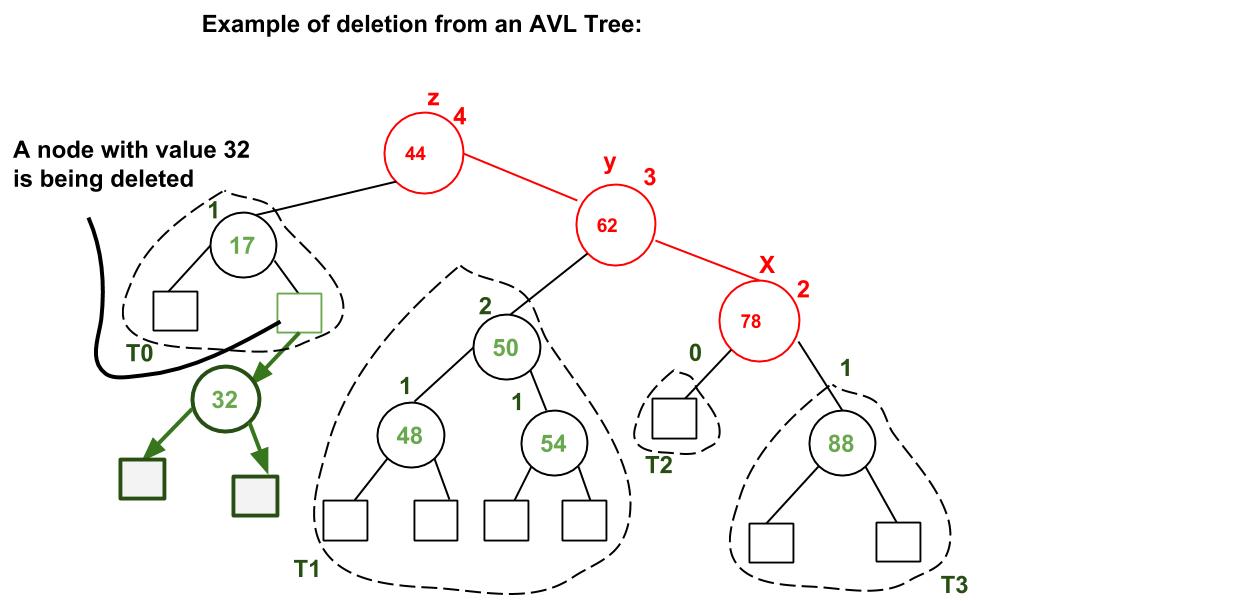
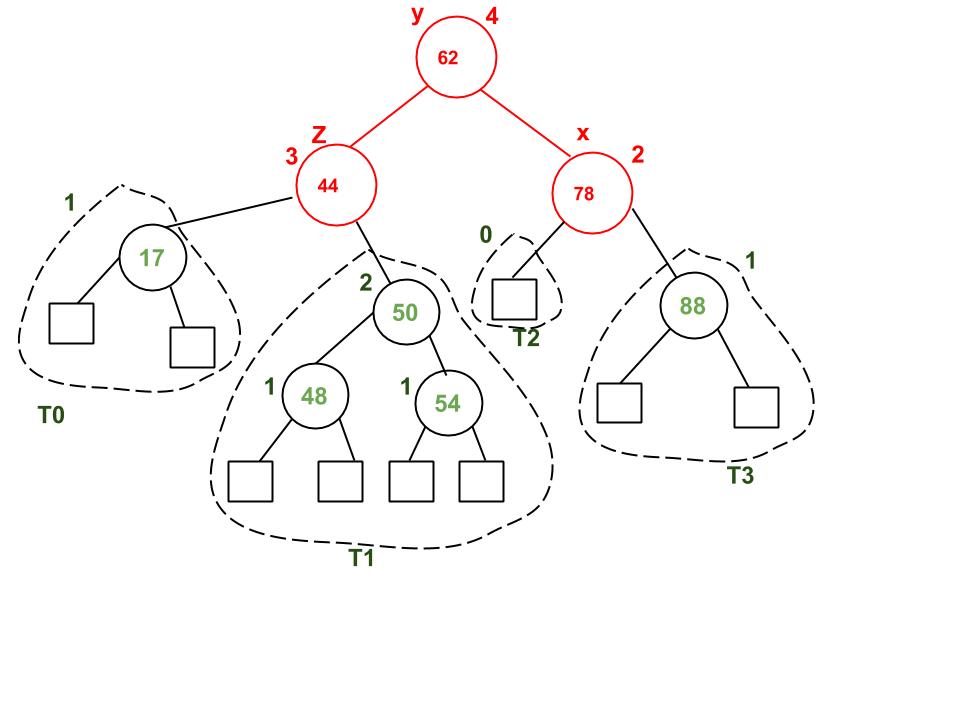 A node with value 32 is being deleted. After deleting 32, we travel up and find the first unbalanaced node which is 44. We mark it as z, its higher height child as y which is 62, and y’s higher height child as x which could be either 78 or 50 as both are of same height. We have considered 78. Now the case is Right Right, so we perform left rotation.
A node with value 32 is being deleted. After deleting 32, we travel up and find the first unbalanaced node which is 44. We mark it as z, its higher height child as y which is 62, and y’s higher height child as x which could be either 78 or 50 as both are of same height. We have considered 78. Now the case is Right Right, so we perform left rotation.
Steps to follow for deletion.
To make sure that the given tree remains AVL after every deletion, we must augment the standard BST delete operation to perform some re-balancing. Following are two basic operations that can be performed to re-balance a BST without violating the BST property (keys(left) < key(root) < keys(right)).
1) Left Rotation
2) Right Rotation
To make sure that the given tree remains AVL after every deletion, we must augment the standard BST delete operation to perform some re-balancing. Following are two basic operations that can be performed to re-balance a BST without violating the BST property (keys(left) < key(root) < keys(right)).
1) Left Rotation
2) Right Rotation
T1, T2 and T3 are subtrees of the tree rooted with y (on left side)
or x (on right side)
y x
/ \ Right Rotation / \
x T3 – - – - – - – > T1 y
/ \ < - - - - - - - / \
T1 T2 Left Rotation T2 T3
Keys in both of the above trees follow the following order
keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
So BST property is not violated anywhere.
Let w be the node to be deleted
1) Perform standard BST delete for w.
2) Starting from w, travel up and find the first unbalanced node. Let z be the first unbalanced node, y be the larger height child of z, and x be the larger height child of y. Note that the definitions of x and y are different from insertion here.
3) Re-balance the tree by performing appropriate rotations on the subtree rooted with z. There can be 4 possible cases that needs to be handled as x, y and z can be arranged in 4 ways. Following are the possible 4 arrangements:
a) y is left child of z and x is left child of y (Left Left Case)
b) y is left child of z and x is right child of y (Left Right Case)
c) y is right child of z and x is right child of y (Right Right Case)
d) y is right child of z and x is left child of y (Right Left Case)
1) Perform standard BST delete for w.
2) Starting from w, travel up and find the first unbalanced node. Let z be the first unbalanced node, y be the larger height child of z, and x be the larger height child of y. Note that the definitions of x and y are different from insertion here.
3) Re-balance the tree by performing appropriate rotations on the subtree rooted with z. There can be 4 possible cases that needs to be handled as x, y and z can be arranged in 4 ways. Following are the possible 4 arrangements:
a) y is left child of z and x is left child of y (Left Left Case)
b) y is left child of z and x is right child of y (Left Right Case)
c) y is right child of z and x is right child of y (Right Right Case)
d) y is right child of z and x is left child of y (Right Left Case)
Like insertion, following are the operations to be performed in above mentioned 4 cases. Note that, unlike insertion, fixing the node z won’t fix the complete AVL tree. After fixing z, we may have to fix ancestors of z as well (See this video lecture for proof)
a) Left Left Case
T1, T2, T3 and T4 are subtrees.
z y
/ \ / \
y T4 Right Rotate (z) x z
/ \ - - - - - - - - -> / \ / \
x T3 T1 T2 T3 T4
/ \
T1 T2
b) Left Right Case
z z x
/ \ / \ / \
y T4 Left Rotate (y) x T4 Right Rotate(z) y z
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
T1 x y T3 T1 T2 T3 T4
/ \ / \
T2 T3 T1 T2
c) Right Right Case
z y
/ \ / \
T1 y Left Rotate(z) z x
/ \ - - - - - - - -> / \ / \
T2 x T1 T2 T3 T4
/ \
T3 T4
d) Right Left Case
z z x
/ \ / \ / \
T1 y Right Rotate (y) T1 x Left Rotate(z) z y
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
x T4 T2 y T1 T2 T3 T4
/ \ / \
T2 T3 T3 T4
Unlike insertion, in deletion, after we perform a rotation at z, we may have to perform a rotation at ancestors of z. Thus, we must continue to trace the path until we reach the root.
Example:



A node with value 32 is being deleted. After deleting 32, we travel up and find the first unbalanaced node which is 44. We mark it as z, its higher height child as y which is 62, and y’s higher height child as x which could be either 78 or 50 as both are of same height. We have considered 78. Now the case is Right Right, so we perform left rotation.
C implementation
Following is the C implementation for AVL Tree. The following C implementation uses the recursive BST delete as basis. In the recursive BST delete, after deletion, we get pointers to all ancestors one by one in bottom up manner. So we don’t need parent pointer to travel up. The recursive code itself travels up and visits all the ancestors of the deleted node.
1) Perform the normal BST insertion and deletion.
2) The current node must be one of the ancestors of the deleted node. Update the height of the current node.
3) Get the balance factor (left subtree height – right subtree height) of the current node.
4) If balance factor is greater than 1, then the current node is unbalanced and we are either in Left Left case or Left Right case. To check whether it is Left Left case or Left Right case, get the balance factor of left subtree. If balance factor of the left subtree is greater than or equal to 0, then it is Left Left case, else Left Right case.
5) If balance factor is less than -1, then the current node is unbalanced and we are either in Right Right case or Right Left case. To check whether it is Right Right case or Right Left case, get the balance factor of right subtree. If the balance factor of the right subtree is smaller than or equal to 0, then it is Right Right case, else Right Left case.
Output:
Preorder traversal of the constructed AVL tree is
9 1 0 -1 5 2 6 10 11
Preorder traversal after deletion of 10
1 0 -1 9 5 2 6 11
Time Complexity: The rotation operations (left and right rotate) take constant time as only a few pointers are being changed there. Updating the height and getting the balance factor also takes constant time. So the time complexity of AVL insert remains same as BST insert which is O(h) where h is the height of the tree. Since AVL tree is balanced, the height is O(Logn). So time complexity of AVL insert is O(Logn).
C implementation
Following is the C implementation for AVL Tree. The following C implementation uses the recursive BST delete as basis. In the recursive BST delete, after deletion, we get pointers to all ancestors one by one in bottom up manner. So we don’t need parent pointer to travel up. The recursive code itself travels up and visits all the ancestors of the deleted node.
1) Perform the normal BST insertion and deletion.
2) The current node must be one of the ancestors of the deleted node. Update the height of the current node.
3) Get the balance factor (left subtree height – right subtree height) of the current node.
4) If balance factor is greater than 1, then the current node is unbalanced and we are either in Left Left case or Left Right case. To check whether it is Left Left case or Left Right case, get the balance factor of left subtree. If balance factor of the left subtree is greater than or equal to 0, then it is Left Left case, else Left Right case.
5) If balance factor is less than -1, then the current node is unbalanced and we are either in Right Right case or Right Left case. To check whether it is Right Right case or Right Left case, get the balance factor of right subtree. If the balance factor of the right subtree is smaller than or equal to 0, then it is Right Right case, else Right Left case.
Following is the C implementation for AVL Tree. The following C implementation uses the recursive BST delete as basis. In the recursive BST delete, after deletion, we get pointers to all ancestors one by one in bottom up manner. So we don’t need parent pointer to travel up. The recursive code itself travels up and visits all the ancestors of the deleted node.
1) Perform the normal BST insertion and deletion.
2) The current node must be one of the ancestors of the deleted node. Update the height of the current node.
3) Get the balance factor (left subtree height – right subtree height) of the current node.
4) If balance factor is greater than 1, then the current node is unbalanced and we are either in Left Left case or Left Right case. To check whether it is Left Left case or Left Right case, get the balance factor of left subtree. If balance factor of the left subtree is greater than or equal to 0, then it is Left Left case, else Left Right case.
5) If balance factor is less than -1, then the current node is unbalanced and we are either in Right Right case or Right Left case. To check whether it is Right Right case or Right Left case, get the balance factor of right subtree. If the balance factor of the right subtree is smaller than or equal to 0, then it is Right Right case, else Right Left case.
Output:
Preorder traversal of the constructed AVL tree is 9 1 0 -1 5 2 6 10 11 Preorder traversal after deletion of 10 1 0 -1 9 5 2 6 11
Time Complexity: The rotation operations (left and right rotate) take constant time as only a few pointers are being changed there. Updating the height and getting the balance factor also takes constant time. So the time complexity of AVL insert remains same as BST insert which is O(h) where h is the height of the tree. Since AVL tree is balanced, the height is O(Logn). So time complexity of AVL insert is O(Logn).
B-Tree
B-Tree is a self-balancing search tree. In most of the other self-balancing search trees (like AVL and Red-Black Trees), it is assumed that everything is in main memory. To understand the use of B-Trees, we must think of the huge amount of data that cannot fit in main memory. When the number of keys is high, the data is read from disk in the form of blocks. Disk access time is very high compared to main memory access time. The main idea of using B-Trees is to reduce the number of disk accesses. Most of the tree operations (search, insert, delete, max, min, ..etc ) require O(h) disk accesses where h is the height of the tree. B-tree is a fat tree. The height of B-Trees is kept low by putting maximum possible keys in a B-Tree node. Generally, a B-Tree node size is kept equal to the disk block size. Since h is low for B-Tree, total disk accesses for most of the operations are reduced significantly compared to balanced Binary Search Trees like AVL Tree, Red-Black Tree, ..etc.
Properties of B-Tree
1) All leaves are at same level.
2) A B-Tree is defined by the term minimum degree ‘t’. The value of t depends upon disk block size.
3) Every node except root must contain at least t-1 keys. Root may contain minimum 1 key.
4) All nodes (including root) may contain at most 2t – 1 keys.
5) Number of children of a node is equal to the number of keys in it plus 1.
6) All keys of a node are sorted in increasing order. The child between two keys k1 and k2 contains all keys in the range from k1 and k2.
7) B-Tree grows and shrinks from the root which is unlike Binary Search Tree. Binary Search Trees grow downward and also shrink from downward.
8) Like other balanced Binary Search Trees, time complexity to search, insert and delete is O(Logn).
Following is an example B-Tree of minimum degree 3. Note that in practical B-Trees, the value of minimum degree is much more than 3.
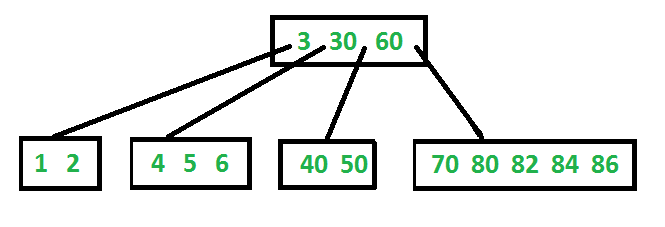
Search
Search is similar to the search in Binary Search Tree. Let the key to be searched be k. We start from the root and recursively traverse down. For every visited non-leaf node, if the node has the key, we simply return the node. Otherwise, we recur down to the appropriate child (The child which is just before the first greater key) of the node. If we reach a leaf node and don’t find k in the leaf node, we return NULL.
Traverse
Traversal is also similar to Inorder traversal of Binary Tree. We start from the leftmost child, recursively print the leftmost child, then repeat the same process for remaining children and keys. In the end, recursively print the rightmost child.
Insert Operation
Since B Tree is a self-balancing tree, you cannot force insert a key into just any node.
The following algorithm applies:
1. Run the search operation and find the appropriate place of insertion.
2. Insert the new key at the proper location, but if the node has a maximum number of keys already:
a. The node, along with a newly inserted key, will split from the middle element.
b. The middle element will become the parent for the other two child nodes.
c. The nodes must re-arrange keys in ascending order.
B-Tree is a self-balancing search tree. In most of the other self-balancing search trees (like AVL and Red-Black Trees), it is assumed that everything is in main memory. To understand the use of B-Trees, we must think of the huge amount of data that cannot fit in main memory. When the number of keys is high, the data is read from disk in the form of blocks. Disk access time is very high compared to main memory access time. The main idea of using B-Trees is to reduce the number of disk accesses. Most of the tree operations (search, insert, delete, max, min, ..etc ) require O(h) disk accesses where h is the height of the tree. B-tree is a fat tree. The height of B-Trees is kept low by putting maximum possible keys in a B-Tree node. Generally, a B-Tree node size is kept equal to the disk block size. Since h is low for B-Tree, total disk accesses for most of the operations are reduced significantly compared to balanced Binary Search Trees like AVL Tree, Red-Black Tree, ..etc.
Properties of B-Tree
1) All leaves are at same level.
2) A B-Tree is defined by the term minimum degree ‘t’. The value of t depends upon disk block size.
3) Every node except root must contain at least t-1 keys. Root may contain minimum 1 key.
4) All nodes (including root) may contain at most 2t – 1 keys.
5) Number of children of a node is equal to the number of keys in it plus 1.
6) All keys of a node are sorted in increasing order. The child between two keys k1 and k2 contains all keys in the range from k1 and k2.
7) B-Tree grows and shrinks from the root which is unlike Binary Search Tree. Binary Search Trees grow downward and also shrink from downward.
8) Like other balanced Binary Search Trees, time complexity to search, insert and delete is O(Logn).
1) All leaves are at same level.
2) A B-Tree is defined by the term minimum degree ‘t’. The value of t depends upon disk block size.
3) Every node except root must contain at least t-1 keys. Root may contain minimum 1 key.
4) All nodes (including root) may contain at most 2t – 1 keys.
5) Number of children of a node is equal to the number of keys in it plus 1.
6) All keys of a node are sorted in increasing order. The child between two keys k1 and k2 contains all keys in the range from k1 and k2.
7) B-Tree grows and shrinks from the root which is unlike Binary Search Tree. Binary Search Trees grow downward and also shrink from downward.
8) Like other balanced Binary Search Trees, time complexity to search, insert and delete is O(Logn).
Following is an example B-Tree of minimum degree 3. Note that in practical B-Trees, the value of minimum degree is much more than 3.


Search
Search is similar to the search in Binary Search Tree. Let the key to be searched be k. We start from the root and recursively traverse down. For every visited non-leaf node, if the node has the key, we simply return the node. Otherwise, we recur down to the appropriate child (The child which is just before the first greater key) of the node. If we reach a leaf node and don’t find k in the leaf node, we return NULL.
Search is similar to the search in Binary Search Tree. Let the key to be searched be k. We start from the root and recursively traverse down. For every visited non-leaf node, if the node has the key, we simply return the node. Otherwise, we recur down to the appropriate child (The child which is just before the first greater key) of the node. If we reach a leaf node and don’t find k in the leaf node, we return NULL.
Traverse
Traversal is also similar to Inorder traversal of Binary Tree. We start from the leftmost child, recursively print the leftmost child, then repeat the same process for remaining children and keys. In the end, recursively print the rightmost child.
Traversal is also similar to Inorder traversal of Binary Tree. We start from the leftmost child, recursively print the leftmost child, then repeat the same process for remaining children and keys. In the end, recursively print the rightmost child.
Insert Operation
Since B Tree is a self-balancing tree, you cannot force insert a key into just any node.
The following algorithm applies:
1. Run the search operation and find the appropriate place of insertion.2. Insert the new key at the proper location, but if the node has a maximum number of keys already:
a. The node, along with a newly inserted key, will split from the middle element.
b. The middle element will become the parent for the other two child nodes.
c. The nodes must re-arrange keys in ascending order.
Delete Operation
The delete operation has more rules than insert and search operations.
The following algorithm applies:
1. Run the search operation and find the target key in the nodes
2. Three conditions applied based on the location of the target key, as explained in the following sections
The delete operation has more rules than insert and search operations.
The following algorithm applies:
1. Run the search operation and find the target key in the nodes
2. Three conditions applied based on the location of the target key, as explained in the following sections
If the target key is in the leaf node
1. Target is in the leaf node, more than min keys.
a. Deleting this will not violate the property of B Tree
2. Target is in leaf node, it has min key nodes
a. Deleting this will violate the property of B Tree
b. Target node can borrow key from immediate left node, or immediate right node (sibling)
c. The sibling will say yes if it has more than minimum number of keys
d. The key will be borrowed from the parent node, the max value will be transferred to a parent, the max value of the parent node will be transferred to the target node, and remove the target value
3. Target is in the leaf node, but no siblings have more than min number of keys
a. Search for key
b. Merge with siblings and the minimum of parent nodes
c. Total keys will be now more than min
d. The target key will be replaced with the minimum of a parent node
1. Target is in the leaf node, more than min keys.
a. Deleting this will not violate the property of B Tree
2. Target is in leaf node, it has min key nodes
a. Deleting this will not violate the property of B Tree
2. Target is in leaf node, it has min key nodes
a. Deleting this will violate the property of B Tree
b. Target node can borrow key from immediate left node, or immediate right node (sibling)
c. The sibling will say yes if it has more than minimum number of keys
d. The key will be borrowed from the parent node, the max value will be transferred to a parent, the max value of the parent node will be transferred to the target node, and remove the target value
3. Target is in the leaf node, but no siblings have more than min number of keys
b. Target node can borrow key from immediate left node, or immediate right node (sibling)
c. The sibling will say yes if it has more than minimum number of keys
d. The key will be borrowed from the parent node, the max value will be transferred to a parent, the max value of the parent node will be transferred to the target node, and remove the target value
3. Target is in the leaf node, but no siblings have more than min number of keys
a. Search for key
b. Merge with siblings and the minimum of parent nodes
c. Total keys will be now more than min
d. The target key will be replaced with the minimum of a parent node
b. Merge with siblings and the minimum of parent nodes
c. Total keys will be now more than min
d. The target key will be replaced with the minimum of a parent node
If the target key is in an internal node
1. Either choose, in- order predecessor or in-order successor
2. In case the of in-order predecessor, the maximum key from its left subtree will be selected
3. In case of in-order successor, the minimum key from its right subtree will be selected
4. If the target key's in-order predecessor has more than the min keys, only then it can replace the target key with the max of the in-order predecessor
5. If the target key's in-order predecessor does not have more than min keys, look for in-order successor's minimum key.
6. If the target key's in-order predecessor and successor both have less than min keys, then merge the predecessor and successor.
If the target key is in an internal node
1. Either choose, in- order predecessor or in-order successor
2. In case the of in-order predecessor, the maximum key from its left subtree will be selected
3. In case of in-order successor, the minimum key from its right subtree will be selected
4. If the target key's in-order predecessor has more than the min keys, only then it can replace the target key with the max of the in-order predecessor
5. If the target key's in-order predecessor does not have more than min keys, look for in-order successor's minimum key.
6. If the target key's in-order predecessor and successor both have less than min keys, then merge the predecessor and successor.
1. Either choose, in- order predecessor or in-order successor
2. In case the of in-order predecessor, the maximum key from its left subtree will be selected
3. In case of in-order successor, the minimum key from its right subtree will be selected
4. If the target key's in-order predecessor has more than the min keys, only then it can replace the target key with the max of the in-order predecessor
5. If the target key's in-order predecessor does not have more than min keys, look for in-order successor's minimum key.
6. If the target key's in-order predecessor and successor both have less than min keys, then merge the predecessor and successor.
If the target key is in a root node
1. Replace with the maximum element of the in-order predecessor subtree
2. If, after deletion, the target has less than min keys, then the target node will borrow max value from its sibling via sibling's parent.
3. The max value of the parent will be taken by a target, but with the nodes of the max value of the sibling.
source:
https://www.geeksforgeeks.org/avl-tree-set-1-insertion/
https://www.geeksforgeeks.org/avl-tree-set-2-deletion/?ref=lbp
https://www.geeksforgeeks.org/introduction-of-b-tree-2/
https://www.guru99.com/b-tree-example.html
1. Replace with the maximum element of the in-order predecessor subtree
2. If, after deletion, the target has less than min keys, then the target node will borrow max value from its sibling via sibling's parent.
3. The max value of the parent will be taken by a target, but with the nodes of the max value of the sibling.
source:
https://www.geeksforgeeks.org/avl-tree-set-1-insertion/
https://www.geeksforgeeks.org/avl-tree-set-2-deletion/?ref=lbp
https://www.geeksforgeeks.org/introduction-of-b-tree-2/
https://www.guru99.com/b-tree-example.html
2. If, after deletion, the target has less than min keys, then the target node will borrow max value from its sibling via sibling's parent.
3. The max value of the parent will be taken by a target, but with the nodes of the max value of the sibling.
https://www.geeksforgeeks.org/avl-tree-set-1-insertion/
https://www.geeksforgeeks.org/avl-tree-set-2-deletion/?ref=lbp
https://www.geeksforgeeks.org/introduction-of-b-tree-2/
https://www.guru99.com/b-tree-example.html

Tidak ada komentar:
Posting Komentar