Binary Search Tree
Binary Search Tree adalah struktur data yang mengadopsi konsep Binary Tree namun terdapat aturan bahwa setiap child node sebelah kiri selalu lebih kecil nilainya dari pada root node. Begitu pula sebaliknya, setiap child node sebelah kanan selalu lebih besar nilainya daripada root node.
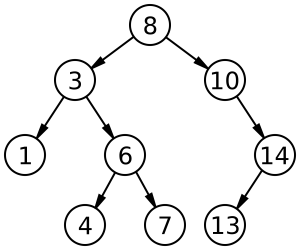
Binary Search Tree membedakan kiri dan kanan sesuai besaran nilainya untuk memberikan efisiensi terhadap proses searching. Kalau struktur data tree sudah tersusun rapi sesuai aturan binary search tree, proses search akan lebih cepat.
Aturan Binary Search Tree:
- Setiap child node sebelah kiri harus lebih kecil nilainya daripada root nodenya.
- Setiap child node sebelah kanan harus lebih besar nilainya daripada root nodenya.
Kemudian, ada 3 jenis cara untuk melakukan penelusuran data (traversal) pada binary search tree, yaitu:
- Pre Order : Print data, telusur ke kiri, telusur ke kanan.
- In Order : Telusur ke kiri, print data, telusur ke kanan.
- Post Order : Telusur ke kiri, telusur ke kanan, print data.
Binary Search Tree memiliki operasi dasar berikut:
- find (X): cari kunci X di Binary Search Tree.
a. Karena properti Binary Search Tree, finding/searching di Binary Search Tree mudah.
b. Biarkan kunci yang ingin kita cari adalah X.
a. Karena properti Binary Search Tree, finding/searching di Binary Search Tree mudah.
b. Biarkan kunci yang ingin kita cari adalah X.
1. Kita mulai dari root.
2. Jika root berisi X maka pencarian berhasil dihentikan.
3. Jika X kurang dari kunci root, maka cari secara rekursif pada sub tree kiri, jika tidak cari
secara rekursif pada sub tree kanan.
- insert (X): masukkan kunci baru X ke dalam Binary Search Tree.
a. Memasukkan ke dalam Binary Search Tree dilakukan secara rekursif.
b. Biarkan kunci node baru menjadi X,
1. Mulailah dari root.
2. Jika X kurang dari kunci simpul maka masukkan X ke sub tree kiri, jika tidak masukkan X
ke sub tree kanan.
3. Ulangi sampai menemukan simpul kosong untuk meletakkan X (X akan selalu menjadi
leaf baru).
- remove (X): hapus kunci X dari Binary Search Tree.b. Biarkan kunci node baru menjadi X,
1. Mulailah dari root.
2. Jika X kurang dari kunci simpul maka masukkan X ke sub tree kiri, jika tidak masukkan X
ke sub tree kanan.
3. Ulangi sampai menemukan simpul kosong untuk meletakkan X (X akan selalu menjadi
leaf baru).
Ada 3 kasus yang harus dipertimbangkan:
1. Jika kunci ada di leaf, hapus saja node itu.
2. Jika kunci ada di node yang memiliki satu children, hapus node itu dan sambungkan
children-nya ke parent-nya.
children-nya ke parent-nya.
3. Jika kunci ada di node yang memiliki dua children, temukan children paling kanan dari sub
tree kirinya (node P), ganti kuncinya dengan kunci P dan hapus P secara rekursif. (atau
secara alternatif dapat memilih anak paling kiri dari sub tree kanannya).
tree kirinya (node P), ganti kuncinya dengan kunci P dan hapus P secara rekursif. (atau
secara alternatif dapat memilih anak paling kiri dari sub tree kanannya).
Contoh Aplikasi Binary Search Tree:
1. Membangun daftar vocabulary yang merupakan bagian dari inverted
index (sebuah struktur
data yang digunakan oleh banyak mesin pencari seperti Google.com, Yahoo.com dan
Ask.com).
data yang digunakan oleh banyak mesin pencari seperti Google.com, Yahoo.com dan
Ask.com).
2. Banyak digunakan dalam bahasa pemrograman untuk mengelola dan
membangun dynamic
sets.
sets.
Pembentukan Binary Search Tree
Bila diketahui sederetan data 5, 3, 7, 1, 4, 6, 8, 9 maka pemasukan data
tersebut dalam struktur data BST, langkah per langkah, adalah sebagai
berikut:
Langkah 1:
Langkah 2:
Pemasukan data 3 disebelah kiri simpul 5 karena 3 < 5.
5
3
5
Struktur Data dan Algoritma 4
Taufik Fuadi Abidin, Irvanizam Zamanhuri, Muhammad Subianto.
Langkah 3:
Langkah 4:
Pemasukan data 1. Karena data 1 lebih kecil dari data di root
yaitu 5 maka penelusuran dilanjutkan kesebelah kiri root.
Kemudian karena disebelah kiri sudah ada daun dengan nilai
3 dan data 1 lebih kecil dari data 3 maka data 1 disisipkan
disebelah kiri simpul 3.
Langkah 5:
Pemasukan data 4.
3
5
7
3
5
7
1
3
5
7
1 4
Struktur Data dan Algoritma 5
Taufik Fuadi Abidin, Irvanizam Zamanhuri, Muhammad Subianto.
Langkah 6:
Pemasukan data 6. Karena data 6 lebih besar dari data di root
yaitu 5 maka penelusuran dilanjutkan kesebelah kanan root.
Kemudian karena disebelah kanan sudah ada simpul dengan
nilai 7 dan data 6 lebih kecil dari data 7 maka data 6
disisipkan disebelah kiri simpul 7.
Langkah 7:
Pemasukan data 8. Karena data 8 lebih besar dari data di root
yaitu 5 maka penelusuran dilanjutkan kesebelah kanan root.
Kemudian karena disebelah kanan sudah ada simpul dengan
nilai 7 dan karena data 8 lebih besar dari data 7 maka data 8
disisipkan disebelah kanan simpul 7.
5
7
6
3
1 4
5
7
6
3
1 4 8
Struktur Data dan Algoritma 6
Taufik Fuadi Abidin, Irvanizam Zamanhuri, Muhammad Subianto.
Langkah 8:
Pemasukan data 9. Karena data 9 lebih besar dari data di root
yaitu 5 maka penelusuran dilanjutkan kesebelah kanan root.
Kemudian karena disebelah kanan bukan merupakan daun
yaitu simpul dengan nilai 7 dan karena data 9 lebih besar dari
data 7 penelusuran terus dilanjutkan kesebelah kanan.
Selanjutnya ditemukan daun dengan nilai 8, karena data 9
lebih besar dari 8 maka data 9 disisipkan disebelah kanan
simpul 8.
5
7
6
3
1 4 8
9.
Berikut adalah contoh implementasi Binary Search Tree pada C beserta searching datanya:#include <stdio.h>
#include <stdlib.h>
//inisialisasi struct
struct data{
int number;
//pointer untuk menampung percabangan kiri dan kanan
data *left, *right;
}*root;
//fungsi push untuk menambah data
void push(data **current, int number){
//jika pointer current kosong maka akan membuat blok data baru
if((*current)==NULL){
(*current) = (struct data *)malloc(sizeof (data));
//mengisi data
(*current)->number=number;
(*current)->left = (*current)->right = NULL;
//jika tidak kosong, maka akan dibandingkan apakah angka yang
//ingin dimasukkan lebih kecil dari pada root
//kalau iya, maka belok ke kiri dan lakukan rekursif
//terus menerus hingga kosong
}else if(number < (*current)->number){
push(&(*current)->left, number);
//jika lebih besar, belok ke kanan
}else if(number >= (*current)->number){
push(&(*current)->right, number);
}
}
//preOrder : cetak, kiri, kanan
void preOrder(data **current){
if((*current)!=NULL){
printf("%d -> ", (*current)->number);
preOrder(&(*current)->left);
preOrder(&(*current)->right);
}
}
//inOrder : kiri, cetak, kanan
void inOrder(data **current){
if((*current)!=NULL){
inOrder(&(*current)->left);
printf("%d -> ", (*current)->number);
inOrder(&(*current)->right);
}
}
//postOrder : kiri, kanan, cetak
void postOrder(data **current){
if((*current)!=NULL){
postOrder(&(*current)->left);
postOrder(&(*current)->right);
printf("%d -> ", (*current)->number);
}
}
//searching data
void search(data **current, int number){
//jika pointer current memiliki data
if((*current)!=NULL){
//cek, apakah datanya lebih kecil. Jika iya, belok ke kiri
if(number<(*current)->number){
search(&(*current)->left,number);
//jika lebih besar, maka belok ke kanan
}else if(number>(*current)->number){
search(&(*current)->right,number);
//jika sama dengan, maka angka ketemu
}else{
printf("Found : %d", (*current)->number);
}
//jika tidak ada data lagi (not found)
}else{
printf("Not Found.");
}
}
int main(){
push(&root, 11);
push(&root, 22);
push(&root, 13);
push(&root, 15);
push(&root, 9);
inOrder(&root);
printf("\n");
preOrder(&root);
printf("\n");
postOrder(&root);
printf("\n");
search(&root,91);
getchar();
}
Source: